U N D E R   C O N S T R U C T I O N

Text by Arne Lüker

This article emerged from a preparation for a job interview


Magnetic Nanoparticles

Introduction
Classification and Definitions
The Problem: Understanding magnetic Nanoparticles in Theory
Notes from Arne´s Lab-book
References

Introduction

The enhanced interest of the researchers in nanoobjects is due to the discovery of unusual physical and chemical properties of these objects, which is related to manifestation of so-called ›quantum size effects‹. These arise in the case where the size of the system is comparable to the de-Brogli wavelengths of the electrons, phonons or excitons propagating in them.
A key reason for the change in the physical and chemical properties of small particles as their size decreases is the increased fraction of the ›surface‹ atoms, which occur under conditions (coordination number, symmetry of the local environment, etc.) differing from those of the bulk atoms. From the energy stand-point, a decrease in the particle size results in an increase in the fraction of the surface energy in its chemical potential.
These unique physical properties of nanoparticles are under intensive research at the moment. A special place belongs to the magnetic properties in which the difference between a massive (bulk) material and a nanomaterial is especially pronounced. In particular, it was shown that magnetisation (per atom) and the magnetic anisotropy of nanoparticles can be much greater than those of a bulk specimen, while differences in the Curie (TC) or Neel (TN) temperatures, i.e., the temperatures of spontaneous parallel or antiparallel orientation of spins, between nanoparticle and the corresponding microscopic phases reach hundreds of degrees. In addition, magnetic nanomaterials were found to possess a number of unusual properties - giant magnetoresistance, abnormally high magnetocaloric effect, and so on.
The magnetic properties of nanoparticles are determined by many factors, the key of these including the chemical composition, the type and the degree of defectiveness of the crystal lattice, the particle size and shape, the morphology (for structurally inhomogeneous particles ), the interaction of the particle with the surrounding matrix and the neighbouring particles. By changing the nanoparticle size, shape, composition and structure, one can control to an extent the magnetic characteristics of the material based on them. However, these factors cannot always be controlled during the synthesis of nanoparticles nearly equal in size and chemical composition; therefore, the properties of nanomaterials of the same type can be markedly different.
The last years have seen changes in the development of magnetic nanomaterials, which can be called revolutionary, to say the least. This is related both to the development of efficient methods for the preparation and stabilsation of nanosized magnetic particles and to the progress in the physical methods for the investigation of such particles.

Magnetic nanoparticles are abundant in nature and are found in many biological objects [1]. Magnetic nanomaterials are used in information recording and storage systems, in new permanent magnets, in magnetic cooling systems, as magnetic sensors, etc. All this accounts for the interest of various specialists in these systems.
Extensive literature is devoted to the applied aspects of the state-of-the-art technology of magnetic recording and its prospects. For instance, powders with micron-size g-Fe2O3, Co-g-Fe2O3, Fe or Fe-Co grains are used most often in magnetic tapes or discs as media for magnetic recording. In this case, recording of one bit requires about 109 atoms [2] whereas with the use of nanomaterials (particles 10 nm in diameter), not more than 105 atoms. Thus, transition to magnetic nanomaterials increases the information recording density by a factor of 103 - 104.
magnetic nanoparticle Among the magnetic materials that have found broad practical application in technology, ferromagnets deserve attention. An important characteristic of a ferromagnet is the coercive force (HC), i.e., the magnetic field strength H corresponding to the point with B = 0 on the symmetric hysteresis loop B(H) of the ferromagnet. Here B is the magnetic field induction in a ferromagnetic sample with zero demagnetising factor (for example, in a long cylinder whose axis is directed along the field). One more characteristic, apart from HC, is the intrinsic coercive force (HCi), defined as the magnetic field strength at the point M = 0 on the symmetric M(H) hysteresis loop of the ferromagnet, where M is the magnetisation of a ferromagnetic sample with zero demagnetising factor. The coercive force and the intrinsic coercive force normally do not differ much in magnitude, but these are different physical quantities. When designing new magnetic materials, it is often a goal to attain the highest HC. Modern magnetic materials have HC = 2 - 3 kŒ In terms of the coercive force, ferromagnets are subdivided into soft magnetic (HC < 12.6 Œ) and hard magnetic (HC > 126 Œ) ones. The magnets with intermediate coercive force values are referred to as semi-hard. Table 1 presents data on the dependence of the magnetic properties of ferromagnets on the dimensions of the constituent particles. Apart from the dimensions, the magnetic properties of particles depend on the external conditions: temperature, pressure and, in some cases, the local environment, i.e., the medium in which the particle occurs, in particular, the crystalline or amorphous bulk matrix (for a particle), the local crystal environment (for a single atom) or the substrate (for a film).
In addition to ferromagnets in which the magnetic moments of the atoms are ordered, magnetic spin glasses - systems in which the competition of random magnetic interactions between magnetic moments results in a magnetic disordered state - also find application in technology.

Classification and Definitions

First of all, it is necessary to consider the general concepts related to the nanosized objects.
A nanoobject is a physical object differing appreciably in properties from the corresponding bulk material and having at least one nanometre dimension (not more than 100 nm). Nanotechnology is the technology dealing with both single nanoobjects and materials and devices based on them and with processes that take place in the nanometre range.
Nanomaterials are those materials whose key physical characteristics are dictated by the nanoobjects they contain. Nanomaterials are classified into compact materials and nanodispersions. The first type includes so-called ›nanostructured‹ materials, i.e., materials isotropic in the macroscopic composition and consisting of contacting nanometre-sized units as repeating structural elements [3]. Unlike nanostructured materials, nanodispersions include a homogeneous dispersion medium (vacuum, gas, liquid or solid) and nanosized inclusions dispersed in this medium and isolated from each other. The distance between the nanoobjects in these dispersions can vary over broad limits from tens of nanometres to fractions of a nanometre. In the latter case, we are dealing with nanopowders whose grains are separated by thin (often monoatomic) layers of light atoms, which prevent them from agglomeration.
A nanoparticle can be seen as a zero-dimensional (0D) nanoobject in which all characteristics linear dimensions are of the same order of magnitude (not more than 100 nm). Nanoparticles can basically differ in their properties from larger particles, for example, from long- and well-known ultradispersed powders with a grain size above 0.5 mm. As a rule of thumb, nanoparticles are shaped like spheroids. Nanoparticles with a clearly ordered arrangement of atoms (or ions) are called nanocrystallites. Nanoparticles with a clear-cut discontinuity of the system of electronic energy levels are often referred to as ›quantum dots‹ or ›artificial atoms‹ (most often, they have compositions of typical semiconductor materials) [4] [5]. The term ›cluster‹, which has been widely used in chemical literature in former years, is currently used to designate small nanoparticles with sizes less than 1 nm. Thus, the term ›nanoclusters‹ is excessive, because all known clusters have nanometre dimensions.
Nanorods and nanowires are quasi-one-dimensional (1D) nano-objects. In these systems, one dimension exceeds by an order of magnitude the other two dimensions, which are in the nano-range. This class includes, in particular, interesting nanostructures such as ›quantum wires‹ [6]. The group of two-dimensional objects (2D) includes planar structures - nanodiscs, thin-film magnetic structures, magnetic nanoparticle layers, etc., in which two dimensions are an order of magnitude greater than the third dimension, which is in the nanometre range.
In this work we consider nanoparticles as giant pseudomolecules having a core and a shell and often also external functional groups. The unique magnetic properties are usually inherent in the particles with a core size of 2 - 30 nm. For magnetic nanoparticles, this value coincides in the order of magnitude with the theoretical estimate for the smallest dimensions of a magnetic domain in most magnetic materials.

Table 1. Type of the change of the magnetic properties of a ferromagnet with a decrease in the substance dimensions from macroscopic to atomic.
  
Macroscopic (bulk)   ³ 1 µm  

spontaneous magnetisation below TC. The appearance of a nonzero magnetic moment is suppressed by the formation of a domain structure
Microscopic   50 - 1000 nm  

magnetic characteristics strongly depend on the sample pre-history, preparation and processing method
Single-domain magnetic particles   1 - 30 nm  

the presence of a blocking temperature Tb < TC below which the magnetic moment of the particle retains orientation in space, while the particle ensemble demonstrates a magnetic hysteresis. At a temperature higher than Tb, the particle transfers into the superparamagnetic state.
In the Tb < T < TC region, the particle has a spontaneous magnetisation and a nonzero total magnetic moment, which easily changes the orientation in the external field
Single atom (ion)   ~ 0.2 nm   usual paramagnetic properties



The Problem: Understanding magnetic Nanoparticles in Theory

It will not be an exaggeration to say that the intensive studies of nanoparticles as a special class of objects started from the discovery of unusual magnetic properties. In 1930, Frenkel and Dorfman showed on the basis of energy considerations that particles of a sufficiently small size should be single-domain. In the mid-20th century, the theory of single-domain particles started to be actively developed [7] [8] [9] [10] [11] [12] and the related phenomena were studied experimentally [13] [14] [15] [16] [17] [18] [19] [20] [21]. These studies identified a substantial increase in the coercive force of a ferromagnet on passing from a multidomain to the single-domain structure, which is important for the creation of permanent magnets. The results of calculations of the characteristic particle size (for different magnetic materials) where the particle becomes single-domain are presented in Table 2. The critical diameter values corresponding to particle transition from the multidomain to the single-domain state presented in the Table were calculated for spherical particles with an axial magnetic anisotropy. For other types of anisotropy (cubic, hexagonal, etc.) and other particle shapes, the numerical estimation of the critical diameter for the single-domain character changes. In particular, the particle can be transferred into the single-domain state without decreasing the volume if it has a shape other than a sphere, for example, an oblong ellipsoid. Experimental determination of the critical diameter above which a single-domain particle becomes multidomain is a too complicated task to be discussed here.

Table 2. Critical diameter (for room temperature) of a single-domain spherical particle with the axial magnetic anisotropy
  
Material   dcrit [nm]      
    from Ref. [37]   from Ref. [31]   from Ref. [25]
Co   70   70   68
Ni   -   55   32
Fe   30   14   12
BaFe12O19   -   -   580
Fe3O4   -   128   -
g-Fe2O3   -   166   -
Nd-Fe-B   200   -   214
SmCo5   1500   55   1528



To put it more exactly, the term ›single-domain‹ does not require a necessary uniform magnetisation throughout the whole particle bulk but only implies the absence of domain walls. In addition, a single-domain particle is not necessarily a ›small‹ particle (as opposed to a ›bulk‹ particle) as regards specific magnetic characteristics. Recent data of a publication [22] demonstrate for instance that a rather large particle can be single-domain but still possessing the physical properties of a bulk material. Thus, the specific properties of nanoparticles start to be manifested at sizes much smaller than the ›single-domain limit‹. It is considered that significant changes in the main physical characteristics of a bulk material appear when the dimensions of its particles decrease to an extent where the ratio of the number of surface atoms NS to the total number N of atoms in the particle approaches 0.5. An interesting formulation of this criterion as applied to magnetic nanoparticles has been proposed. Assuming that in a surface layer of thickness Dr (defectiveness parameter), the number of exchange bonds is twice as low as that in the particle bulk and that the Curie temperature is directly proportional to the bulk density of exchange bonds, Nikolaev and Shipilin [23] have analysed the dependence of TC on the magnetite particle size obtained earlier [22]. The defectiveness parameter Dr was found to depend on the particle radius r. In particular, for magnetite Dr ® 0 for r ® 2.5 nm (the radius for the single-domain state of magnetite is ~70 nm, see Table 2). As the particle radius decreases, the parameter Dr substantially increases and for r = 2.5 nm, it amounts to 0.5 nm. Thus, the smaller the magnetic particle size, the greater the effective depth to which the violation of the regular structure extends.

One more remarkable property of the nanoparticles, which allowed their experimental discovery in the mid-20th century, is the superparamagnetism. The higher the particle magnetic moment, the lower the magnetic field HS that is required to observe the magnetisation saturation phenomenon. In a rough approximation, the HS value (saturation field) can be estimated from the formula

mef ⋅ HS   »   kB ⋅ T


where mef is the effective magnetic moment of the particle. For paramagnetic Gd(SO4)3⋅H2O, the effective magnetic moment of the Gd3+ ion is for instance 7 mB. Thus, the HS value for this paramagnet at room temperature would be HS » 300 kB/7 » 106 Œ. For a particle with an effective magnetic moment of 104 mB, the saturation field would decrease to 103 Œ.
The phenomenon of saturation of the magnetisation curve in low (for a usual laboratory) fields of ~1 kŒ has been called ›superparamagnetism‹, while a material exhibiting such properties is called a ›superparamagnetic‹.
The model of an ideal superparamagnetic was mainly worked out by the early 1960s [24], but now it seems to get new attention [25] [26]. The simplest variant of this model considers a system of N non-interacting identical particles with the magnetic moment mef. Since the magnetic moment of the particle is assumed to be large, its interaction with the magnetic field H is calculated without taking the quantum effects into account. In the case of isotropic particles, the equilibrium magnetisation of the áMñ system is described by the Langevin equation

áMñ   =   N mef [coth (mef H/kB T) - kB T/mef H]       (Eq.: 1)


Equation (1) has been derived with the assumption that single particles are magnetically isotropic, i.e., all directions for their magnetic moments are energetically equivalent, but this condition is hardly ever fulfilled. If the particles are magnetically anisotropic, the calculation of the equilibrium magnetisation becomes more complicated. According to the nature of factors giving rise to the non-equivalence of the directions of magnetic moments, one can distinguish the magnetically crystalline anisotropy; the shape anisotropy; anisotropy associated with the internal stress and external impact; exchange anisotropy, and so on [27].
For nanoparticles, the surface magnetic anisotropy plays a special role. Unlike other kinds of magnetic anisotropy, the surface anisotropy is proportional to the surface area of the particle S rather than to its volume V. The surface anisotropy appears due to the violation of the symmetry of the local environment and the change in the crystal field, which acts on magnetic ions located on the surface. Uniaxial anisotropy is the simplest type of magnetic anisotropy as regards the symmetry properties. In the general case, the equation for the energy of the uniaxial magnetic anisotropy is written as the sum of two contributions:

E(q)   =   (KV V + KS S) sin2q       (Eq.: 2)


where KV is the volume anisotropy constant, V is the particle volume, KS is the surface anisotropy constant, q is the angle between the vector of the particle magnetic moment m and the anisotropy axis.

When the surface makes no contribution to the anisotropy, the angular dependence of the particle energy has the form

E(q)   =   KV V sin2q


If no external magnetic field or surface anisotropy are present, the minimum energy of the particle is attained at the orientation of the magnetic moment m along the anisotropy axis. In this case, two neighbouring minima are separated by a barrier with height KV V. In an external magnetic field H applied at the angle y to the anisotropy axis, the particle energy is equal to

E(q)   =   KV V sin2q   -   MS VH cos(q - y)       (Eq.: 3)


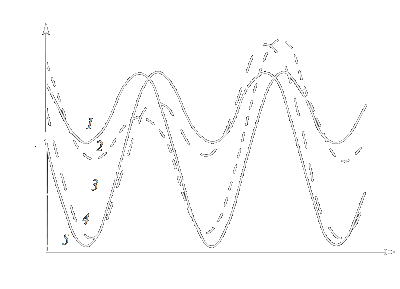Figure 1: Angular dependence of the energy of a uniaxial magnetic particle B(q) at different orientations of the external magnetic field H. y = 180 (1), 135 (2), 90 (3), 35 (4), 0 (5).
(The particle is assumed to be uniformly magnetised to saturation, its magnetic moment being m = MS V.) The dependence of the particle energy on the angle q for different angles y is shown in Fig. 1 for KV = 4.5 105 J/m3, V = 103 nm3, MS = 1.4 106 A/m, H = 105 A/m. It can be seen that in the vicinity of q = 0, p and 2p, there are three energy minima separated by non-equivalent barriers [in the case of y = 0 and p (curves 1 and 5), the barriers are equivalent].
In the general case, in the presence of an external magnetic field, rotation of the magnetic moment of the particle to reach the orientation corresponding to an energy minimum requires overcoming an energy barrier, DE = KVV. The relation for the characteristic time of thermal fluctuations of the magnetic moment of a single-domain particle with a uniaxial anisotropy provided that DE/kBT ³ 1 was obtained by Néel [28].

t   =   t0 ⋅ e DE/kBT       (Eq.: 4)


Later on, this expression was extended by Brown [9] [10] [11] [12] to the cubic anisotropy case.
The pre-exponential factor t0 depends on many parameters including temperature, gyromagnetic ratios, saturation magnetisation, anisotropy constants, the height of energy barrier, and so on [29] [30]. However, for the sake of simplicity t0 is often considered to be a constant in the range of 10-9 - 10-13 s [31].
Equation (4) determines the characteristic time needed for the thermal equilibrium in a system of non-interacting single-domain magnetic particles to establish. At higher temperatures, DE/kBT « 1; the time required for system transition into a state with the minimum energy is short compared to the characteristic time of measurements tmeas, and the system is not expected to show a magnetic hysteresis. In the case where DE/kBT » 1, the system transition into an equilibrium state may take a very long time depending appreciably on the particle. For t0 = 10-9 s, KV = 105 J/m3 and T = 300 K for a magnetically anisotropic spherical particle 11.4 nm in diameter, we get t = 10-1 s and for a particle with a diameter of 14.6 nm, t = 108 s [31].
If tmeas » t, the system occurs in the superparamagnetic state and rapidly reaches an equilibrium magnetisation on changing the temperature or the external field. Otherwise (tmeas « t), after a change in the external magnetic field, the system does not arrive to a new equilibrium state over the time tmeas and its magnetisation does not change. The case t = tmeas in relation (4) corresponds to the blocking temperature Tb. If tmeas = 100 s (characteristic time for the static magnetic measurements) and t0 = 10-9 s, the condition tmeas = t in relation (4) gives KVV » 25.3 kB T. Hence,

Tb   =   KV V / 25 kB       (Eq.: 5)


It is noteworthy that relation (5) specifies the blocking temperature for a zero magnetic field. As the external magnetic field is enhanced, the blocking temperature decreases by a power law

Tb(H)   =   Tb(0) [1 - (H / HC)]k       (Eq.: 6)



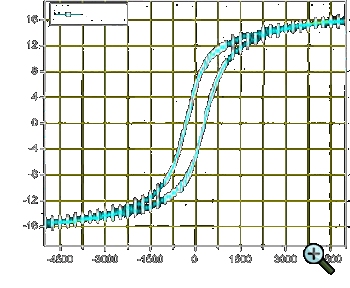Figure 2: Magnetisation vs. magnetic field hysteresis curve at room-temperature for a sample of Cu-Ni-Fe nanocomposites
where k = 2 (for low fields [32]) and 2/3 (for high fields [33]), HC = 2K/MS.
The experimental data obtained for magnetite nanoparticles show that upon an increase in the field from zero to 700 Œ, the blocking temperature decreases from 140 to 75 K, relation (6) being fulfilled rather accurately below 50 Œ with k = 2, and for fields from 50 to 700 Œ, with k = 2/3 [34].
When investigating the magnetic properties of the samples containing nanoparticles, the magnetisation curve is usually measured up to saturation magnetisation (Fig. 2) [35]. To determine the temperature dependence of the magnetic moment m, two types of measurements are carried out, namely, zero-field cooling (ZFC) and field cooling (FC). According to the ZFC procedure, the sample is cooled (usually down to the liquid helium temperature) in the absence of a magnetic field and then a moderate measuring field is applied (1 - 100 Œ) and the temperature is gradually raised, the magnetic moment mZFC values being recorded. The FC procedure differs from ZFC only by the fact that the sample is cooled in a nonzero magnetic field. For magnetic nanoparticles, the mFC(T) and mZFC(T) curves usually coincide at relatively high temperatures but start to differ below a certain temperature Tir (irreversibility temperature). The mZFC(T) curve has a maximum at some temperature Tmax, and the mFC(T) curve, most often, ascends monotonically to very low temperatures (Fig. 3). The dependence of magnetisation on the applied field at various temperatures is often additionally measured. Electron magnetic resonance and Mössbauer spectroscopy data are also used for analysis of the magnetic properties.
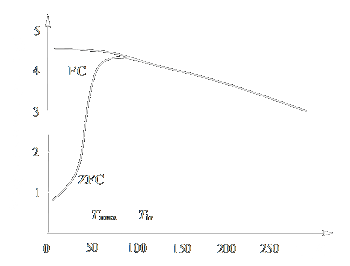Figure 3: Temperature dependences of the magnetic moment (ZFC and FC measurements)
For an idealised system containing identical nanoparticles with uniaxial anisotropy and a random orientation of easy magnetisation axes, the difference between the temperature dependences of mFC and mZFC at a qualitative level follows from Eq. 3 and Fig. 1. In the case of a zero field, on cooling below the blocking temperature, the magnetic moments of particles are oriented along their easy magnetisation axes [q = y = 0 in Eq. 3], the total magnetic moment of the system being equal to zero both at the beginning and at the end of cooling. After the external field H has been switched on, the magnetic moments for which q - y < 90° [see Eq. 3] do not need to overcome an energy barrier and they rotate to the minimum-energy position, thus creating a non-zero magnetisation. For example, for the curve y = 35° in Fig. 1, the rotation angle will be 29°. Conversely, the magnetic moments for which q - y > 90° on switching on the magnetic field are separated from the energy minimum by a potential barrier which they can overcome only over a long period of time [see Eq. 4]. Therefore, in the case of ZFC measurements for T < Tb, the system gets into a metastable state with a relatively low total magnetic moment MS2H/3KV, which does not depend on the temperature [36]. When T = Tb, the system passes via a jump into a stable superparamagnetic state with the magnetic moment

mZFC   =   MS2 ⋅ VH / 3kBT       (Eq.: 7)


For MS⋅VH || kBT and a random orientation of the axes of easy magnetisation of particles, relation (7) holds also for T > Tb [37]. In the FC-measurements, cooling of the sample takes place in a nonzero magnetic field; at any temperature above Tb, magnetisation is determined by Eq (7). When T < Tb, the system magnetisation can no longer change over the time of measurements. Therefore, the magnetic moment in the FC procedure at T < Tb is equal to

mFC   »   MS2 ⋅ VH / 3kBT   =   const.


For a system consisting of single-domain nanoparticles with a size, shape, etc. dispersions, the mZFC(T) and mFC(T) curves are not separated at T = Tb, but are separated at a higher temperature Tir > Tb, which is called the irreversibility point [38]. Another characteristic point in the mZFC(T) curve is the temperature Tmax, which is often identified as the average temperature of system blocking áTbñ. For a temperature below áTbñ, an increase in mFC(T) is observed, which is then replaced by a ›saturation‹ section and in some cases, by a maximum [37]. The Tir value can be identified with the blocking temperature for the largest particles, and Tmax, with the blocking temperature for the smallest particles. However, it should be borne in mind that all these characteristic temperatures (and their relationship with the volume distribution of particles) can depend on the rate of sample cooling and subsequent heating [39] and on the intensity of the interparticle interactions. If the rate of sample heating is much lower than the cooling rate, the mFC(T) may have a maximum at T < áTbñ [37]. In the case of strong interparticle interactions, the energy distribution of particles DE [see Eq. (2)] may narrow down (in relative units s/m, where s is the dispersion, m is the average value) with respect to the volume distribution [37]. In this case, a more accurate calculation of the local magnetic field acting on a single particle is required.
Note that the mZFC(T) and mFC(T) curves differ not only for the systems of magnetic nanoparticles but also for macroscopic magnets with disorder elements (exchange coupling frustration, topological disorder, structural defects) and even in ordered ferromagnets with a substantial magnetic anisotropy [40].
The difficulty of the theoretical investigation of the magnetic hysteresis in nanoparticles lies in the fact that this non-linear, non-equilibrium and non-local phenomenon caused by the existence of energy minima (resulting from the magnetic anisotropy) and the barriers separating them depends, in a complex manner, on the external magnetic field. The results of theoretical studies using relatively simple models seldom provide a plausible description for real magnetic nanomaterials as they do not take into account their microstructure, in particular, the effect of boundaries and defects on the local magnetisation [41].
An important role of the microstructure in the formation of magnetic characteristics is indicated by the studies of nanocomposite materials (for example, the Nd-Fe-B/a-Fe system [42] or the Cu-Ni-Fe system, which should be the heart of this study), which represent a magnetically soft medium with nano-sized grains distributed therein (< 100 nm) [43]. In these materials, the magnetically hard phase ensures a high coercive force, while the magnetically soft phase provides a high saturation magnetisation. In addition, the substantial exchange interaction between the grains ensures a relative residual magnetisation higher than 0.7. Therefore, materials of this type are called exchange-coupled magnets. In recent years attempts have been undertaken to study the effect of the internal structure (microstructure) of a nanoparticle on the magnetic characteristics of real nanomaterials.
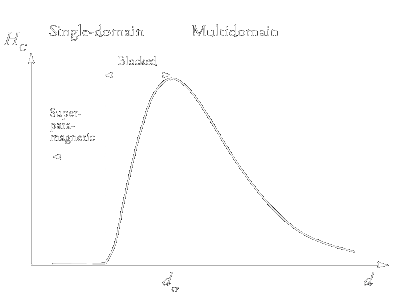Figure 5: Qualitative dependences of the coercive force HC on the particle diameter.
Most successful was the use of numerical calculations within the framework of the micromagnetism theory (so-called ›computer micro-magnetism‹) [44] [45] [46] [47]. Even when a nanoparticle has a defect-free crystal structure, the different local environments of atoms at the particle boundary and inside the particle result in a nonuniform magnetisation in the particle and distortion of the perfect collinear magnetic structure [48] [49]. The calculations show that at the final temperature, magnetisation decreases along the direction from the particle centre toward the boundary [50], and the magnetic moment of each particular surface atom can be greater than that of the bulk atoms [51]. The decrease in the magnetisation on the particle surface compared to that in the bulk is due a lower energy of the surface spin wave excitations [26], in other words, more pronounced action of the thermal fluctuations on the surface. The increase in the magnetic moment of surface atoms can be attributed, within the framework of the band theory, to the decrease in the coordination number, and, as a consequence, to narrowing the corresponding energy band and an increase in the density of states. Apparently, this also accounts for the rare cases of magnetic order appearing in metal nanoparticles whose bulk analogues are non-magnetic [52] [53] [54] [55].
The qualitative isothermal dependence of the coercive force HC on the characteristic size of magnetic particles is shown in Fig. 5. The increase in HC upon a decrease in the particle size follows from the Stoner-Wohlfarth theory according to which the spins of atoms forming a nanoparticle rotate coherently, i.e., concertedly. It is known from experiments that the coercive force in real magnetic materials (including nanomaterials) is much lower than the limiting values predicted by the theory even at very low temperatures. One reason is that under the action of an external magnetic field, the spins of the atoms forming the nanoparticle can rotate not only coherently but also in a more complex manner to form spin modes: ›swirls‹, ›fans‹, etc. [25]. The appearance of non-coherent spin modes is facilitated if nanoparticles form agglomerates (for example, chains). The coherent rotation can, apparently, take place only in absolutely defect-free uniform particles with a zero surface anisotropy. It is evident by intuition that the coercive force should be the lower the greater the number of options (mechanisms) for spin rotation in the direction opposite to the initial one. In a multidomain particle, this rotation can be additionally associated with the displacement of domain boundaries. As the particle size decreases, the number of domains decreases, and the role of interdomain boundaries in magnetisation reversal becomes less pronounced. Therefore, up to the critical particle size (dcr, see Fig. 5), the coercive force increases with a decrease in d. However, further decrease in the particle size and transition to single-domain particles entails an increase in the role of thermal fluctuations. This explains a decrease in HC at d < dcr (see Fig. 5).
Important information on the magnetic properties of nanoparticles and material based on them can be derived from measurements of slow relaxation processes [26] [37] [45] [56]. In the simplest cases, for a system of identical magnetic nanoparticles, the equilibrium magnetisation upon the change in the magnetic field (for example, quick switching off) is described by the equation

M(t)   =   M0 ⋅ e-t/t       (Eq.: 8)


where the relaxation time t is determined by the equation (4).
For low-temperature measurements of the residual magnetisation of systems containing magnetic nanoparticles which can exist in the blocked state, three types of experimental procedures are used [57]. During the measurements of isothermal residual magnetisation (IRM), the sample is cooled in a zero magnetic field; after that, the field H is first applied and then switched off at a constant temperature T. In this case, the residual magnetisation of MIRM depends on the H and T values. In the measurements of the thermal residual magnetisation MTRM, the sample is placed in a constant magnetic field H at a high temperature (when all particles are superparamagnetic) and then cooled to low temperature and the field is switched off. Finally, the DC demagnetisation is measured in the same way as MIRM, but the sample is first magnetised to saturation at low temperature, then the field H is switched on in the opposite direction and then switched off. In the absence of interparticle interactions [34]

MDCD(H)   =   MIRM(∞) - 2MIRM(H)       (Eq.: 9)


The non-observance of this rule is considered to indicate the presence of interaction between the particles [58], although for a particle with mixed anisotropy (for example, uniaxial + cubic), this conclusion should be used with caution [59].
For real systems, the function f(E) of particle distribution over the heights of the energy barrier always has a finite width, which is associated with the size, shape, morphology and composition differences between the particles. In this case, the relaxation properties of a system cannot be described using one parameter. For a rectangular distribution f(E), the simple equation (8) should be replaced by the following relation [31]

M(t)   =   M0 - S ln (t/t0)       (Eq.: 10)


where S is the magnetic viscosity coefficient.
If the applied external magnetic field H varies at a constant temperature, the maximum magnetic viscosity coefficient is attained at H = HC. The logarithmic law (10) is usually confirmed experimentally only for relatively short observation periods [37]. The deviations from the logarithmic law can provide information on the symmetry of magnetic anisotropy, size distribution of particles, and so on.
Taking account of magnetic interactions between nanoparticles is a complicated theoretical task. In a quite interesting discussion [37] [60] [61] dealing with the effect of interparticle interactions on the blocking temperature, two models were proposed, one predicting an increase in Tb [61], whereas the other, conversely, a decrease in Tb [37] following an enhancement of the interparticle interactions. The interactions change the height of the energy barrier separating two states of a particle with the opposite directions of the magnetic moment. If the barrier grows, Tb increases and vice versa. The influence of the change in the distances between the maghemite nanoparticles with a diameter of 6-7 nm on the blocking temperature has been studied experimentally [62]. The distances between the particles were changed by compacting the sample. The maximum increase in the sample density was 55%; simultaneously, Tb [corresponding to the maximum in the curve mZFC(T)] increased from 50 to 80 K. Assuming that for noncharged nanoparticles, the predominant magnetic dipole-dipole interactions are inversely proportional to the cubed distance between the particles, one can expect a linear dependence of Tb on the sample density. This is in good agreement with a publication [62].
Figure 6: Scheme of the possible transitions in a system of magnetic nanoparticles arranged randomly in space taking into account interparticle interactions.
(1) Transition from the paramagnetic to superparamagnetic state within single particles; (2) transition from the superparamagnetic into ›blocked‹ state; (3) transition from the ›blocked‹ state into a ›spin glass‹ type state; (4) transition from the superparamagnetic state to a ›spin glass‹ type state.
In the presence of interparticle interactions, the qualitative picture of the behaviour of a system of magnetic nanoparticles following a decrease in temperature may become more complicated than the mere transition to the blocked state [63]. The possible transitions are shown in Fig. 6. If the particles are arranged irregularly in space, the interparticle interactions should transfer the system into the ›spin glass‹ type state at some temperature Tg [63]. Which of the temperatures, either Tg or the average blocking temperature áTbñ would be higher for the given type of particles depends on the particle size and on the average distance between them. Since the temperature dependences of the magnetic moment (ZFC - FC) for a system of non-interacting particles and for a ›spin glass‹ are similar [64], determination of the nature of the transition is a non-trivial task.
To choose theoretically between these states, one first has to know the way of estimating the interacting force in the nanoparticle system. Often, it is assumed that the interparticle interactions can be neglected if the particle concentration in the matrix is low and, hence, the average distance between them is rather high (1.5 times higher than the average particle diameter) [57]. This assumption can be proved by verifying experimentally the fulfillment of relation (9).
In 2001 [65], an interesting approach to taking account of the effect of interparticle interactions on the magnetisation curves of nanoparticles has been proposed. On the basis of the monotonic decrease in mef with a decrease in temperature observed experimentally, the researchers cited introduced phenomenological corrections into relation (1). It was assumed that the magnetic dipole-dipole interactions, which predominate in the systems under consideration, act as a random factor and prevent magnetisation (ordering) of the system, i.e., function in the same way as the temperature. It is worth noting that, although the proposed approach is strictly applicable only to equilibrium systems, it describes satisfactorily the magnetisation curves at any temperatures, including those below the blocking temperature Tb [in this case, the average value over two branches of the hysteresis loop should be taken as M(H)]. The applicability of this model for T < Tb is apparently due to the predominance of interparticle interactions over one-particle effects for all the samples studied.

Notes from Arne´s Lab-book:

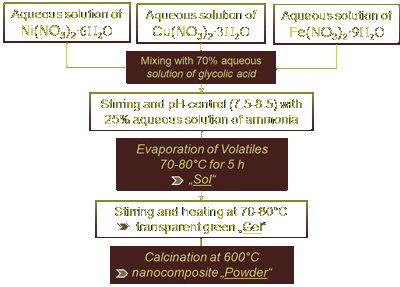Figure 7: Sol-Gel preparation of Cu-Ni-Fe nanocomposites
A ›magnetisation vs. magnetic field hysteresis curve‹ for a Cu-Ni-Fe nanocomposite was already shown in Fig. 2. The nanocomposite was synthesised via the so-called Sol-Gel-route, a wet chemical route that is ideal for colloidal materials like nanoparticles and nanocomposites. It is relatively inexpensive and flexible both in terms of substrate-sizes and stoichiometric compositions. For instance, the sample whose hysteresis is shown in Fig. 2 had a Cu-Ni-Fe-ratio of ~33:33:33, simply speaking it is an easy task to adjust this ration to 20:40:40 or 60:10:30 and so on. Fig. 7 illustrates the Sol-Gel process [66]. The particle size of the nanocomposite was estimated using a Zetasizer and found to be in the range of 10-120 nm, viz. based on Table 2 the critical particle size dcr can be found in between this range. Taking control over the particle size enables the proof of concept behind Fig. 4.
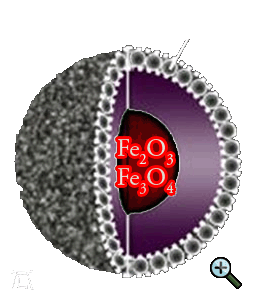
At the time the Cu-Ni-Fe nanocomposite was made, the structure itself was not of interest. For obvious reasons it is of great importance now, so let us catch up on this.

For a start it is believed, that Fe forms the FexOy core of the nanocomposite and Cu/Ni is forming the shell at one ratio or that there is a Fe-Ni alloy existing as a core at another ratio with Cu forming the shell. A Fe-Cu core at one ratio is not an option, because Fe and Cu are immiscible. A pure iron-core is as well nearly impossible in this arrangement, because Fe always contains oxides, carbides and other impurities. Among the first option we have for instance Fe2O3, Fe3O4 (magnetite), FeO (wustite), a-FeOOH (goethite) as a possible core, all with different characteristics. Let us have a look at them:
    Among several crystalline modifications of Fe2O3, there are two magnetic phases, namely, rhombohedral a-Fe2O3 (hematite) and cubic g-Fe2O3 (maghemite) phases. In the a-Fe2O3 structure, all Fe3+ ions have an octahedral coordination, whereas in g-Fe2O3 having the structure of a cation-deficient AB2O4 spinel, the metal atoms A and B occur in tetrahedral and octahedral environments, respectively.
    The oxide a-Fe2O3 is antiferromagnetic (soft magnetic) at temperatures below 950 K, while above the Morin point (260 K) it exhibits so-called ›weak‹ ferromagnetism. The a-Fe2O3 and FeOOH (goethite) nanoparticles are obtained by controlled hydrolysis of Fe3+ salts [67]. In order to avoid the formation of other phases, a solution of ammonia is added to a boiling aqueous solution of Fe(NO3)3 with intensive stirring. Boiling for 2.5 h and treatment of the precipitate with ammonium oxalate (to remove the impurities of other oxides) affords a red powder containing a-Fe2O3 nanoparticles (20 nm) [68]. These nanoparticles are also formed on treatment of solutions of iron salts (Fe2+ : Fe3+ = 1 : 2) with an aqueous solution of ammonium hydroxide in air [69].

    A bulk g-Fe2O3 sample is a ferrimagnet (hard magnetic) below 620°C. The g-Fe2O3 nanoparticles (4 - 16 nm) with a relatively narrow size distribution have been obtained [70] by mild oxidation (on treatment with Me3NO) of pre-formed metallic nanoparticles. The same result can be attained by direct introduction of Fe(CO)5 into a heated solution of Me3NO. The oxidation with air oxygen is alsoused to prepare g-Fe2O3 nanoparticles. For this purpose, the Fe3O4 nanoparticles (9 nm) are boiled in water at pH 12 - 13 [71].
    The most popular route to g-Fe2O3 nanoparticles is thermal decomposition of Fe3+ salts in various media. Rather exotic groups are used in some cases as anions. For example, good results have been obtained by using iron complexes with cupferron [72]. Special-purity g-Fe2O3 is formed upon vaporisation of iron(III) oxide in a solar furnace with subsequent condensation [73] [74]. A mechanochemical synthesis of g-Fe2O3 has been described [75]. An iron powder was milled in a planetary mill with water. During milling, the Fe atoms displace hydrogen from water and are converted into g-Fe2O3. The researchers consider that this is a convenient one-stage synthesis of maghemite nanoparticles (15 nm).

    The cubic spinel Fe3O4 (magnetite) is ferrimagnetic (soft magnetic) at temperatures below 858 K. The route to these particles used most often involves treatment of a solution of a mixture of iron salts (Fe2+ and Fe3+) with a base under an inert atmosphere. For example, the addition of an aqueous solution of ammonia to a solution of FeCl2 and FeCl3 (1 : 2) yields nanoparticles, which are transferred into a hexane solution by treatment with oleic acid [76]. The repeated selective precipitation gives Fe3O4 nanoparticles with a rather narrow size distribution. The synthesis can be performed starting only from FeCl2, but in this case, a specified amount of an oxidant (NaNO2) should be added to the aqueous solution apart from alkali. This method allows one to vary both the particle size (6.5 - 38 nm) and (to a certain extent) the particle shape [77].
    In some cases, thermal decomposition of compounds containing Fe3+ ions under oxygen-deficient conditions is accompanied by partial reduction of Fe3+ to Fe2+. Thus thermolysis of Fe(acac)3 in diphenylether in the presence of small amounts of hexadecane-1,2-diol (probable reducer of a part of Fe3+ ions to Fe2+) gives very fine Fe3O4 nanoparticles (about 1 nm), which can be enlarged by adding excess Fe(acac)3 into the reaction mixture [78]. For partial reduction of Fe3+ ions, hydrazine has been recommended [79]. The reaction of Fe(acac)3 with hydrazine is carried out in the presence of a surfactant. This procedure resulted in superparamagnetic magnetite nanoparticles with controlled sizes, 8 and 11 nm.
    The controlled reduction of ultradispersed a-Fe2O3 in a hydrogen stream at 723 K (15 min) is a more reliable method of synthesis of Fe3O4 nanoparticles. Particles with ~13 nm size were prepared in this way [80].

    Cubic Fe2+ oxide - FeO (wustite) - is antiferromagnetic (TC = 185 K) in the bulk state. Joint milling of Fe and Fe2O3 powders taken in a definite ratio gave nanoparticles (5 - 10 nm) consisting of FeO and Fe [81]. On heating of these particles at temperatures of 250 - 400°C, the metastable FeO phase disproportionates to Fe3O4 and Fe, while above 550°C it is again converted into nanocrystalline FeO [82] [83].

    Among the known oxide hydroxides Fe2O3⋅H2O, the orthorhombic a-FeOOH (goethite) is antiferromagnetic in the bulk state and has TC = 393 K [84], b-FeOOH (akagenite) is paramagnetic at 300 K [85], g-FeOOH (lipidocrokite) is paramagnetic at 300 K and d-FeOOH (ferroxyhite) is ferrimagnetic [86]. Although the bulk a-FeOOH is antiferromagnetic, in the form of nanoparticles it has a nonzero magnetic moment due to the incomplete compensation of the magnetic moments of the sublattices [87]. As a rule, a-FeOOH is present in iron nanoparticles as an admixture phase.
In our Cu-Ni-Fe-system the formation of a Fe2O3 or Fe3O4 core over a wide Cu:Ni:Fe-ratio range is most likely. There is still another option for another ratio:
    The bulk samples of the Fe-Ni alloys are either nonmagnetic or are magnetically soft ferromagnets (for example, permalloys containing >30% of Ni and various doping additives). When the content of nickel is ~30%, their magnetic properties approach the properties of invar (36% of Ni, 64% of Fe, about 0.05% of C). The Fe-Ni nanoparticles have a much lower saturation magnetisation than the corresponding bulk samples over the whole concentration range [88]. An alloy containing 37% of Ni has a low TC and a FCC structure. It consists of nanoparticles (12-80 nm) superparamagnetic over a broad temperature range [89]. Theoretical calculations predict a complex magnetic structure for these Fe-Ni particles (clusters).
For simplicity and reasons of maximum likelihood it is believed that we have a Fe2O3/Fe3O4 core with a Ni/Cu shell. Fig. 2 shows this configuration together with a corresponding SAED pattern and HR-TEM micrograph [66] [90].
With other words, we have a soft magnetic core, which provides a high saturation magnetisation, with a relative hard magnetic shell - which ensures a high coercive force - surrounding it.

References:

  1. R. Frankel, R. Blakemore and R. Wolfe, Science 203, p. 1355, 1979.
  2. J. Bucher and L. Bloomfield, J. Mod. Phys. B 7, p. 1076, 1993.
  3. A. Gusev and A. Rampel, Nanocrystalline Materials, Moscow: Fizmatlit, 2001.
  4. R. Turton, The Quantum Dot, Oxford: Spectrum, 2000.
  5. K. Wang and A. Balandin, Quantum Dots: Physics and Applications in Optics of Nanostructured Materials, 2001: Wiley, New York.
  6. J. Hu, T. Odom and C. Lieber, Acc. Chem. Res. 32, p. 435, 1999.
  7. C. Kittel, Phys. Rev. 70, p. 965, 1946.
  8. E. Stoner and E. Wohlfarth, Philos. Trans. R. Soc. London, A240, p. 599, 1948.
  9. W. Brown Jr, Appl. Phys. 29 , p. 470, 1958.
  10. W. Brown Jr, J. Appl. Phys. 30, p. 130, 1959.
  11. W. Brown Jr, J. Appl. Phys. 34, p. 1319, 1963.
  12. W. Brown Jr, Phys. Rev. B 130, p. 1677, 1963.
  13. V. Gottschalk, Physics 6, p. 127, 1935.
  14. W. Elmor, Phys. Rev. 54, p. 309, 1938.
  15. W. Elmor, Phys. Rev. 54, p. 1092, 1938.
  16. F. Bitter, A. Kaufmann, C. Starr and S. Pan, Phys. Rev. 60, p. 134, 1941.
  17. A. Mayer and E. Vogt, Z. Naturforsch., A, p. 334, 1952.
  18. W. Heukolom, J. Broeder and L. Van Reijen, J. Chim. Phys. 51, p. 51, 1954.
  19. C. Bean, J. Appl. Phys. 26, p. 1381, 1955.
  20. C. Bean and I. Jacobs, J. Appl. Phys. 27 , p. 1448, 1955.
  21. E. Kneller and F. Luborsky, J. Appl. Phys. 34, p. 656, 1963.
  22. B. Sadeh, M. Doi, T. Shimizu and M. Matsui, J. Magn. Soc. Jpn. 24, p. 511, 2000.
  23. V. Nikolaev and A. Shipilin, Fiz. Tv. Tela 45, p. 1029, 2003.
  24. I. Jacobs and C. Bean, in Magnetism Vol. 3, New York, Academic Press, 1963, p. 271.
  25. S. Skomski, J. Phys.: Condens. Matter 15, p. R841, 2003.
  26. X. Batlle and A. Labarta, J. Phys. D 35, p. R15, 2002.
  27. S. Chikazumi, Physics of Ferromagnetism, Magnetic Characteristics and Engineering Applications Vol. 2, Tokyo: Shokabo Publ. Co., 1984.
  28. L. Néel, C.R. Hebd. Seances Acad. Sci. 5, p. 99, 1949.
  29. W. Coffey, D. Crothers, J. Dormann, L. Geoghegan, Y. P. Kalmykov, J. Waldron and A. Wickstead, J. Magn. Magn. Mater. 145, p. L263, 1995.
  30. W. Coffey, D. Crothers, J. Dormann, L. Geoghegan, Y. P. Kalmykov, J. Waldron and A. Wickstead, Phys. Rev. B 52, p. 15951, 1995.
  31. D. Leslie-Pelecky and R. Rieke, Chem. Mater. 8, p. 1770, 1996.
  32. E. Wohlfarth, J. Phys. 10, p. 241, 1980.
  33. L. Wenger and J. Mydosh, Phys. Rev. B 29 , p. 4159, 1984.
  34. W. Chantrell and K. O'Grady, in Applied Magnetism, Dordrecht, Boston, London, Kluwer Academic, 1992, p. 113.
  35. A. Lüker, "Hysteresis of ferromagnetic Cu-Ni-Fe nanocomposites," Research Notes 4261, 2010.
  36. S. Sappey, E. Vincent, N. Hadacek, F. Chaput, J. Boilot and D. Zins, Phys. Rev. B 56, p. 551, 1997.
  37. J. Dormann, D. Fiorani and E. Tronc, Adv. Chem. Phys. 98, p. 283, 1997.
  38. M. Hansen and S. Mørup, J. Magn. Magn. Mater. 203, p. 214, 1999.
  39. R. Chantrell and E. Wohlfarth, Phys. Status Solidi A 91, p. 619, 1985.
  40. P. Joy, P. Kumar and S. Date, J. Phys.: Condens. Matter. 10, p. 11049, 1998.
  41. W. Wernsdorfer, D. Mailly and A. Benoit, J. Appl. Phys. 87, p. 5094, 2000.
  42. J. Jakubowicz and M. Giersig, J. Alloys Compd. 349, p. 311, 2003.
  43. G. Hadjipanayis, J. Magn. Magn. Mater. 200, p. 373, 1999.
  44. J. Fidler and T. Schrefl, J. Magn. Magn. Mater. 177, p. 970, 1998.
  45. R. Fischer and H. Kronmuller, J. Magn. Magn. Mater. 184, p. 166, 1998.
  46. R. Kodama, A. Berkowitz, E. McNiff and S. Foner, Phys. Rev. Lett. 77, p. 394, 1996.
  47. R. Kodama, A. Berkowitz, E. McNiff and S. Foner, J. Appl.Phys. 81, p. 5552, 1997.
  48. O. Iglesias and A. Labarta, Phys. Rev. B 63 , p. 184416, 2001.
  49. H. Kachkachi, M. Noguès, E. Tronc and D. Garanin, J. Magn. Magn. Mater. 221 , p. 158, 2000.
  50. P. Hendriksen, S. Linderoth and P.-A. Lindgård, Phys. Rev. B 48, p. 7259, 1993.
  51. F. Liu, M. Press, S. Khanna and P. Jena, Phys. Rev. B 39, p. 6914, 1989.
  52. S.-K. Ma and J. Lue, Solid State Commun. 97, p. 979, 1996.
  53. T. Taniyama, E. Ohta and T. Sato, Physica B 237 , p. 286, 1997.
  54. T. Nakano, Y. Ikemoto and Y. Nozue, J. Magn. Magn. Mater. 226, p. 238, 2001.
  55. B. Reddy, S. Khanna and B. Dunlap, Phys. Rev. Lett. 70, p. 3323, 1993.
  56. K. O'Grady and R. Chantrell, in Magnetic Properties of Fine Particles, Amsterdam, Elsevier, 1992, p. 93.
  57. J. Dormann, F. D'Orazio, F. F Lucari, E. E Tronc, P. Prené, J. Jolivet, D. Fiorani, R. Cherkaoui and M. Noguès, Phys. Rev. B 53, p. 14291, 1996.
  58. E. Wohlfarth, J. Magn. Magn. Mater. 39, p. 39, 1983.
  59. J. Geshev, M. Mikhov and J. Schmidt, J. Appl. Phys. 85, p. 4321, 1999.
  60. J. Dormann, L. Bessais and D. Fiorani, J. Phys. C: Solid State Phys. 21, p. 2015, 1988.
  61. M. Hansen and S. Mørup, J. Magn. Magn. Mater. 184, p. 262, 1998.
  62. J. Dai, J.-Q. Wang, C. Sangregorio, J. Fang, E. Carpenter and J. J Tang, J. Appl. Phys. 87, p. 7397, 2000.
  63. S. Mørup, Europhys. Lett. 28, p. 671, 1994.
  64. W. Luo, S. Nagel, T. Rosenbaum and R. Rosensweig, Phys. Rev. Lett. 67, p. 2721, 1991.
  65. P. Allia, M. Coisson, P. Tiberto, F. Vinai, M. Knobel, M. Novak and W. Nunes, Phys. Rev. V 64, p. 144420, 2001.
  66. A. Lüker, "Sol-gel route of ferromagnetic Cu-Ni-Fe nanocomposites," Research Notes 4159, 2009.
  67. U. Schwertmann and E. E Murad, Clays Clay Miner. 31, p. 277, 1983.
  68. M. Hansen, C. C B Koch and S. P. R. B. 6. Mørup, Phys. Rev. B 62, p. 1124, 2000.
  69. L. Zhang, G. Papaefthymiou and J. Ying, "1997," J. Appl. Phys. 81, p. 6892.
  70. T. Hyeon, S. Lee, J. Park, Y. Chung and H. Na, J. Am. Chem. Soc. 123, p. 798, 2001.
  71. J. Tang, M. Myers, K. Bosnick and L. Brus, J. Phys. Chem. B 107, p. 7501, 2003.
  72. J. J Rockenberger, E. Scher and A. Alivisatos, J. Am. Chem. Soc. 121 , p. 11595, 1999.
  73. B. Martinez, X. Obradors, L. Balcells, A. Rouanet and C. Monty, Phys. Rev. Lett. 80, p. 181, 1988.
  74. A. Rouanet, H. Solmon, G. Pichelin, C. Roucau, F. Sibieude and C. Monty, Nanostruct. Mater. 6, p. 283, 1995.
  75. R. R Janot and D. Guerard, J. Alloys Compd. 333, p. 302, 2002.
  76. T. Fried, G. Shemer and G. Markovich, Adv. Mater. 13, p. 1158, 2001.
  77. I. Nedkov, T. Merodiiska, S. Kolev, K. Krezhov, D. Niarchos, E. Moraitakis, Y. Kusano and J. Takada, Monatsh. Chem. 133, p. 823, 2002.
  78. S. S Sun and H. Zeng, J. Am. Chem. Soc. 124, p. 8204, 2002.
  79. Y. Hou, J. Yu and S. Gao, J. Mater. Chem. 13, p. 1983, 2003.
  80. R. Panda, N. Gajbhiye and G. Balaji, J. Alloys Compd. 326, p. 50, 2001.
  81. J. Ding, W. Miao, E. Pirault, R. Street and P. McCormick, J. Alloys Compd. 267, p. 199, 1998.
  82. L. Minervini and R. Grimes, J. Phys. Chem. Solids 60, p. 235, 1999.
  83. K. K Tokumitsu and T. Nasu, Scr. Metall. 44, p. 1421, 2001.
  84. C. Koch, M. Madsen and S. S Mørup, Hyperfine Interact. 28, p. 549, 1986.
  85. S. Mørup, T. Meaz, C. Koch and H. Hansen, Z. Phys. D 40, p. 167, 1997.
  86. T. Meaz, C. Koch and S. Mørup, Proceedings of the Conference ICAME-95, Bologna, Vol. 50, p. 525, 1996.
  87. M. Madsen and S. Mørup, Hyperfine Interact. 42, p. 1059, 1988.
  88. X. Li, A. Chiba and S. Takahashi, J. Magn. Magn. Mater. 170, p. 339, 1997.
  89. A. Afanas'ev, I. Suzdalev, M. Ya Gen, V. Gol'danskii, V. Korneev and E. Manykin, J. Exp. Theor. Phys. 58, p. 115, 1970.
  90. M. Srivastava, A. Ojha, S. Chaubey, P. Sharma and A. Pandey, Mater. Chem. Phys. 120, p. 493, 2010.

[ back ]