Die sich ergebende Kutve besäße alsdann die Gleichung

Stifel prägte hier für die Zahlen der oberen Reihe ein Wort, das sich seitdem in der Mathematik Bürgerrecht erworben hat, das Wort Exponent, weil diese Zahlen, wie anfangs erwähnt, aus den Potenzen "herausgesetzt", exponiert worden sind. Unter der Gegenüberstellung der beiden Reihen findet sich auf lateinisch ein bedeutsamer Satz, der in deutscher Übersetzung lautet:

»Es wäre möglich, hier ein fast ganz neues Buch über die wunderbaren Eigenschaften dieser Zahlen zu schreiben. Aber ich muss mich hinwegschleichen und mit geschlossenen Augen von dannen gehen.«

1. Es handelt sich beispielsweise um des Produkt 2³ ⋅ 2⁵! Es kommt 2⁸ heraus; denn es gilt:
   
   
   2³ ⋅ 2⁵ = (2 ⋅ 2 ⋅ 2) ⋅ (2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2) = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 2⁸

   Potenzen mit derselben Basis werden also multipliziert, indem man ihre Exponenten addiert:
   
   

   Potenzrechnung		23		⋅		25		=		28
   Exponentrechnung		3		+		5		=		8

   
   Eine Addition zweier Exponenten bedeutet also eine Multiplikation zweier Potenzen mit derselben Basis.
   



2. Aus allem dem geht ohne weiters hervor, dass Potenzen mit gleicher Basis dividiert werden, indem man ihre Exponenten subtrahiert, z.B.:
   
   

   Potenzrechnung		28		:		23		=		25
   Exponentrechnung		8		-		3		=		5

   
   Eine Subtraktion zweier Exponenten bedeutet also eine Division zweier Potenzen mit derselben Basis.
   



3. Nun liegt es nahe, aufzusuchen, worauf wohl eine Multiplikation zweier Exponenten zurückweist. Das wird uns klar, wenn wir uns etwa die Aufgabe (2³)⁵ vornehmen. Heraus kommt 2¹⁵. Denn es gilt:
   
   
   (2³)⁵ = 2³ ⋅ 2³ ⋅ 2³ ⋅ 2³ ⋅ 2³ = 2¹⁵

   Eine Potenz wird allso nochmals potenziert, indem man den alten Exponenten mit dem neuen Exponenten multipliziert:
   
   

   Potenzrechnung		(23)5		=		215
   Exponentrechnung		3 ⋅ 5		=		15

   
   Eine Multiplikation zweier Exponenten bedeutet also eine nochmalige Potenzierung einer Potenz.
   



4. Worauf weist nunwohl eine Division zweier Exponenten zurück? Das enthüllt sich einem erst, wenn man das Potenzieren rückwärts beherrscht. Erhebe ich z.B. die Basis 4 in die 3. Potenz, so rechne ich 4 ⋅ 4 ⋅ 4 aus, indem ich, von der 4 ausgehend, zunächst 4 ⋅ 4 = 16 berechne und dann noch 16 ⋅ 4 = 64 ermittel. Man durchschreitet also bei der Potenzierung von 4 die einzelnen Potenzen von 4 bis 64 hin. Nehmen wir nun das Bild des Baumes aus Abschnitt 1 wieder auf: Die Aufgabe 4³ = 64 bedeutet, den Baum vom Stamm zur Krone hin zu durchlaufen; denn wir enden mit der Kronenzahl 64. Dieses Potenzieren rückwärts betreiben, würde bedeuten, aus der Kronenzahl 64 durch ein dreimaliges Dividieren zur 1, also zur Stammzahl, zurückzugelangen. Das geht nur, wenn man die 64 dreimal durch 4 dividiert:
   
   

   64 : 4		=		16
   16 : 4		=		4
   4 : 4		=		1

   
   Man durchläuft also bei einem rückwärtigen Potenzieren den Baum von der Krone zum Stamm und damit zur Wurzel hin. Darum nennt man das rückwärtige Potenzieren auch Wurzelberechnung oder Radizieren (von lat. radix = Wurzel). Ob man sagt:
   
   

   		4, in die 3. Potenz erhoben, ergibt 64
   oder		64, in die 3. Wurzel versetzt, ergibt 4

   
   bleibt sich gleich. Man kann in der Schreibweise den Vorwärtsprozess vom Rückwärtsprozess folgendermaßen unterscheiden:
   
   

   43		=		64
   364		=		4

   
   Man setzte also den Exponenten nicht rechts oben, sondern links oben hin. Zum Überfluss fügen Mathematiker noch den Buchstaben r als Anfangsbuchstaben des Wortes radix links hinzu, um das Rückwärtsrechnen zu unterstreichen:
   
   

   		3r64		=		4
   oder stilisiert		3√64		=		4

   
   Wahrscheinlich entstand das Wurzelzeichen √ im Laufe der Zeit aus dem schludrig und nachlässig geschriebenen r, aber das sei hier nur geraten. Wie dem auch sei, wenn wir also nun noch 64 und 4 als Potenzen von 2 schreiben, wird daraus:
   
   

   ³√2⁶ = 2²

   Eine Potenz wird also radiziert, indem man ihren Exponenten durch den Exponenten der Wurzel dividiert:
   
   

   Potenzrechnung		3√26		=		26 :3		=		22
   Exponentrechnung		6 : 3		=		2

   
   Eine Division zweier Exponenten bedeutet also eine Radizierung einer Potenz.

Wir erkennen aus dieser Gegenüberstellung, dass deim Übergang von den Potenzen zu ihren Exponenten sich die Rechnungsart in eine um zwei Stufen niedrigere und leichtere verwandelt.Außerdem ersehen wir, dass dem Addieren und dem Subtrahieren von Potenzen auf der Seite der Exponenten nichts entspricht. Eine Vereinfachung der beiden untersten Stufen des Rechnens um zwei Stufen ist ja schlechterdings undenkbar. Diese Unmöglichkeit hängt im Grunde damit zusammen, dass die Potenzen Gebilde darstellen, welche aus der Rechnungsart der Multiplikation hervorwachsen, ist doch die Potenz 4³ nichts weiter ais die Muliplikation 4 &sdot 4 &sdot 4. So ist es verständlich, dass die Potenzen mit der Multiplikation und ihrer Rückwendung, der Division, leicht und mühelos eine Verbindung eingehen; Multiplikation und Division von Potenzen gleicher Basis sind wie Verbindungen chemisch verwandter Elemente. Dem Addieren und seiner Rückwendung, dem Subtrahieren, stehen dagegen die Potenzen verhältnismäßig fern; die Summe 2³ + 2⁵ ist nicht wieder eine Potenz von 2.
Es ist nun nicht mehr nötig, sich mit dem schwierigen Multiplikationen, Divisionen, Potenzieren und Radizieren herumzuplagen. Der bloße Übergang von den Potenzen zu ihren Exponenten macht daraus Addition, Subtraktion, Multiplikation und Division. Diese Eigenschaft der Exponenten, das praktische Rechnen zu erleichtern, lässt es gerechtfertigt erscheinen, ihnen einen neuen Namen zu geben, der diese Eigenschaft ausdrückt; man kann sie Ersatzzahlen nennen. Die Potenzen sind die Zahlen, mit denen das Rechnen schwierig ist; die Exponenten sind ihre Ersatzzahlen, mit denen das Rechnen leichter wird. Statt von Potenzen und ihren Exponenten zu sprechen, kann man einfach von Zahlen und ihren Ersatzzahlen sprechen. So ist z.B. 5 die Ersatzzahl der Zahl 32 unter Zugrundelegung der Basis 2, weil eben 2⁵ = 32 ist, 3 die Ersatzzahl der Zahl 8 unter Zugrundelegung der Basis 2, weil eben 2³ = 8 ist,

Statt der Worte Zahl und Ersatzzahl bedient man sich in der Mathematik zweier Fremdwörter gleichen Sinnes, der Worte Numerus (Zahl) und Logarithmus (Ersatzzahl). Das erstere von beiden ist ohne weiteres verständlich. Das letztere bedarf erst noch der Erklärung, die wir jedoch zunächst noch aufschieben. Unter Zugrundelegung dieser beiden Fachausdrücke, die sich in der Mathematik seit etwa vier Jahrhunderten eingebürgert haben, müssen wir in unseren beiden Beispielen sagen:

Die neue Schreibweise kürzt man natürlich ab:

Zwischen den drei Zahlen des ersten Beispiels, 2, 5 und 32, besteht eine Rechenbeziehung, welche nunmehr auf dreifache Art ausgedrückt werden kann:

Außer diesen Verknüpfungsarten der drei Zahlen 2, 5 und 32 kann es weitere geben. Die Wurzelrechnung ergab sich uns als eine Rückwendung des Potenzierens. Wir lernen nun daneben eine andere Rückwendung desselben Potenzierens kennen, das Logarithmieren, d.h. den Ursprung von einer Zahl zu ihrer Ersatzzahl, von einem Numerus zu seinem Logarithmus.
Es war wenige Jahre nach Stifel's Tode, dass man an Hand eines Reihenpaares ähnlich dem, wie es auch uns vorgelegen hat, dem Ersatzzahlcharakter der Glieder der einen Reihe auf die Spur kam. Am Beginn des 17. Jahrhunderts entdeckten sogar zwei Mathematiker, der Schweizer Joost Bürgi und der Schotte Lord Neper, fast gleichzeitig und unabhängig voneinander die hier dargelegten Zusammenhänge. Lord Neper war es dann auch, der im Jahre 1614 in seiner Abhandlung "Mirfici logarithmorum canonis descriptio" (Beschreibung des wunderbaren Verzeichnisses der Logarithmen) die Bezeichnungen Numerus und Logarithmus schuf. Bei ihm hat das Wort Logarithmus noch den Sinn von Verhältnis-Zahl; die Wahl des Wortes erklärt sich aus dem Berechnungsverfahren, durch das er zu dieser Zahl gelangte. Das Wort Logarithmus setzt sich ja aus den beiden griechischen Worten logos und arithmos zusammen. Ersteres drückte dem Griechen ein Verhältnis zweier Zahlen aus, wie es uns z.B. in der Steigung einer schrägen Strecke entgegentrat, wogegen letzteres die Zahl schlechthin bezeichnet. Der Weg, den Lord Neper einschlug, war verschlungen und führte durch viel Gestrüpp hindurch, ehe das Neuland mit freiem Überblick überschaut werden konnte. Erst allmählich wurde man sich des Zusammenhanges des Logarithmus mit der Potenz und der Wurzel bewusst, und so war es erst Euler im Jahre 1748, der das Logarithmieren als eine neben der Wurzelrechnung bestehenden zweite Umkehrung des Potenzierens kennzeichnete, so, wie es heute durchgängig anerkannt und gelehrt wird. Aber mit dieser Klärung der Anschauung hat das von Lord Neper unter anderem Aspekte eingeführte Wort Logarithmus nicht etwa seinen Sinn eingebüßt, im Gegenteil, dieser Sinn kann noch vertieft werden. Das Wortpaar logos und arithmos kommt nämlich im Griechischen auch als zusammengehöriges Begriffspaar zur Kennzeichnung eines ganz bestimmten Gegensatzes vor: unter logos verstand der alte Grieche auch die Zahl, sofern sie ein Gebilde des praktischen Lebens, des praktischen Rechnens war; die selbe Zahl wurde für ihn zum arithmos, wenn es sich um eine wissenschaftliche Erkenntnis, um wissenschaftliche Erforschung der Zahlen handelte. Noch um die Zeitenwende herum unterschied man in Griechenland die Logistik von der Arithmetik und meinte mit der ersteren die praktische Rechenkunst, mit der letzteren das, was in der mathematischen Wissenschaft heute die Zahlentheorie ist. Das Wort Logarithmus schließt nun beide Seiten der Zahl zu einer schönen Einheit zusammen, und das mit Recht, weil die Exponenten nicht nur Zahlengebilde von rein theoretischem Interesse, also arithmoi, darstellen, sondern auch als Ersatzzahlen der Numeri außerordentlich geeignet für die Rechenpraxis und damit logoi sind.
Mit Hilfe der neuen Symbolik sind wir nun auch in der Lage, die Vereinfachung der Rechnungsarten beim Übergang von den Potenzen zu den Exponenten, von den Numeri zu den Logarithmen, auf neue Art, in Gestalt von Vereinfachungsformeln, auszudrücken. Es wird ja solcher Formeln vier geben müssen. Um sie zu gewinnen, wollen wir unser Reihenpaar noch einmal hinschreiben:

1. Addition von Exponenten
   Wir greifen beispielsweise die Summe der beiden Exponenten 3 und 5 heraus:
   
   

   3

   +

   5

   =

   8

   
   Nun schreiben wir jede der drei Exponenten in den Logarithmus ihres Numerus um:
   
   

   3		=		log 8
   5		=		log 32
   8		=		log 256

   
   Es gilt also:
   
   

   log 8

   +

   log 32

   =

   log 256

   
   Die drei Numeri 8, 32 und 256 hängen aber miteinander durch Multiplikation zusammen:
   
   

   8

   ⋅

   32

   =

   256

   
   So erhalten wir:
   
   

   log 8

   +

   log 32

   =

   log (8 ⋅ 32)

   
   Für beliebige Numeri a und b würde gelten:
   
   

   log a

   +

   log b

   =

   log (a ⋅ b)

   
   Das ist die erste Vereinfachungsformel, die den Tatbestand wiedergibt: Eine Addition zweier Exponenten entspricht einer Multiplikation zweier Potenzen.
   



2. Subtraktion von Exponenten
   Wir greifen beispielsweise die Differenz der beiden Exponenten 8 und 5 heraus:
   
   

   8

   -

   5

   =

   3

   
   Wieder schreiben wir jede der drei Exponenten in den Logarithmus ihres Numerus um:
   
   

   8		=		log 256
   5		=		log 32
   8		=		log 8

   
   Es gilt also auch:
   
   

   log 256

   -

   log 32

   =

   log 8

   
   Die drei Numeri 256, 32 und 8 sind miteinander durch Division verbunden:
   
   

   256

   :

   32

   =

   8

   
   So erhalten wir:
   
   

   log 256

   -

   log 32

   =

   log (256 : 32)

   
   Für beliebige Numeri a und b würde gelten:
   
   

   log a

   -

   log b

   =

   log (a : b)

   
   Das ist die zweite Vereinfachungsformel, die den Tatbestand wiedergibt: Eine Subtraktion zweier Exponenten entspricht einer Division zweier Potenzen.
   



3. Multiplikation von Exponenten
   Wir bilden beispielsweise das Produkt der beiden Exponenten 2 und 3:
   
   

   2

   ⋅

   3

   =

   6

   
   Wieder führen wir für jede der drei Exponenten den Logarithmus des entsprechenden Numerus ein:
   
   

   2		=		log 4
   3		=		log 8
   6		=		log 64

   
   Es gilt demnach auch:
   
   

   log 4

   ⋅

   log 8

   =

   log 64

   
   Die drei Numeri 256, 32 und 8 sind aber nicht miteinander rechnerisch verbindbar. Also springt in diesem Fall keine solche Vereinfachungsformel wie bei der Addition und der Subtraktion von Exponenten heraus. Wohl aber kommen wir auch hier weiter, wenn wir von den Exponenten 2 und 3 nur eine derselben, etwa die 3, in den Logarithmus ihres Numerus umschreiben; dann erhalten wir:
   
   

   2

   ⋅

   log 8

   =

   log 64

   
   Die drei Zahlen 2, 8 und 64 sind aber rechnerisch verbunden:
   
   

   82

   =

   64

   
   Es gilt demnach auch:
   
   

   2 ⋅ log 8

   =

   log (82)

   
   Für beliebige Zahlen a und n würde wir erhalten haben:
   
   

   n ⋅ log a

   =

   log (an)

   
   Das ist die dritte Vereinfachungsformel, die den Tatbestand wiedergibt: Eine Multiplikation zweier Exponenten entspricht einer Potenzierung einer Potenz.
   



4. Division von Exponenten
   Wir bilden beispielsweise den Quotienten der beiden Exponenten 6 und 3:
   
   

   6

   :

   2

   =

   3

   
   Wieder würden wir in eine Sackgasse geraten, wenn wir jede der drei Exponenten in den Logarithmus ihres Numerus umschreiben. Wir kommen jedoch weiter, wenn wir die Exponenten 6 und 3 umschreiben:
   
   

   6		=		log 64
   3		=		log 8

   
   Durch Einsetzen erhalten wir:
   
   

   2√(64)

   =

   8

   
   So erhalten wir:
   
   

   log 64

   :

   2

   =

   log 2√(64)

   
   Für zwei beliebige Zahlen a und n würden wir erhalten haben:
   
   

   log a

   :

   n

   =

   log n√a

   
   Für zwei beliebige Zahlenchungsformel, die den Tatbestand wiedergibt: Eine Division zweier Exponenten entspricht einer Radizierung einer Potenz.

In diesen vier Formeln ist die stillschweigende Voraussetzung gemacht, dass von der linken Seite jeder Gleichung zur rechten Seite die Basis festgehalten wird.
Eine Vereinfachung der beiden untersten und leichtesten Rechnungsarten, der Addition und der Subtraktion, existiert nicht, wie schon auseinandergesetzt wurde. Deshalb fallen auch die Formeln für den Logarithmus einer Summe oder einer Differenz aus:

Die Versuchung liegt nahe, gedankenlos folgende Formeln zu verwenden:

Vor ihrer Aufstellung sei ausdrücklich gewarnt; würden auch sie gelten, so müsste die Summe a + b mit dem Produkt a ⋅ b und die Differenz a - b mit dem Quotienten a : b identisch sein. Für die Logarithmen einer Summe oder einer Differenz gibt es durchaus Formeln; aber sie lauten wesentlich anders und sind nur durch höhere Mathematik erlangbar, sie sind sogar für die Berechnung der Logarithmen von grundlegender Wichtigkeit. Aber für unsere elementar gehaltene Betrachtung scheiden sie aus.

6. Vervollkommnung des Reihenpaares

Alle Zahlen zwischen 1 und 2 lassen sich als Dezimalzahlen mit der 1 vor dem Komma schreiben; wir wissen also:

Es fragt sich nur noch, wie die Stellen hinter dem Komma lauten. Diese lassen sich auf mehrfache Art ermitteln; wir beschränken uns auf das elementare Verfahren.
Wir bilden eine möglichst hohe Potenz von 3, etwa 3²⁰, und untersuchen, zwischen welchen Potenzen von 2 sie liegt:

Mithin liegt log (3²⁰) zwischen 31 und 32. Wäre die Kurve, welche unsere Potenzreihe verbildlicht, zwischen den Hochzahlen 31 und 32 nicht krumm, sondern gerade, so ließe sich sagen: genau so, wie 3²⁰ zwischen 2³¹ und 2³² liegt, ist log (3²⁰) zwischen 31 und 32 gelegen. Was damit gemeint ist, veranschaulicht die Grafik zur Linken, in der ganz links noch der Buchstabe "O" zu denken ist.
Vom Exponenten 0 (Null) bis zum Exponenten 31 auf der waagerechten Gerade sei die Strecke OA, vom Exponenten 0 (Null) bis zum Exponenten 32 die Strecke OC. Dann ist:

In A ist die Länge AD = 2³¹ = 2 147 483 648 als Senkrechte errichtet;
in C ist die Länge CF = 2³² = 4 294 967 296 als Senkrechte errichtet.
Unsere Kurve geht also Durch D und F mit einer leichten Krümmung dazwischen. Diese Krümmeng wollen wir jedoch vernachlässigen und die Kurve zwischen D und F als gerade annehmen. Dann nimmt die Senkrechte BE = 3²⁰ = 3 486 784 401 zwischen den Senkrechten AD und CF eine bestimmte Lage ein, und es muß sich verhalten:

Mithin ist:

Andererseits wissen wir, dass

Also gilt:

In dem Maße, wie unsere Kurve zwischen D und F durch E hindurch von der Gerade abweicht, weicht der soeben errechnete Wert von log 3 von dem wirklichen Werte ab. Da der Kurvenbogen von D nach F etwas nach unten durchhängt, muss der Punkt E und mit ihm der Punkt B etwas weiter rechts liegen, d.h. log 3 muss in Wahrheit etwas größer als der berechnete Wert sein. Eine genauere Rechnung, deren Grundlagen wir hier, an dieser Stelle, nicht auseinandersetzen wollen, würde dementsprechend ergeben:

die Punkte deuten an, dass noch weitere Zahlen folgen und zwar, wie hier zu begründen übergangen werden muss, unendlich viele.
Durch unser Verfahren haben wir also log 3 auf der Basis 2 bereits auf 2 Dezimalstellen genau berechnen können. Dieses Verfahren wollen wir das Proportionalverfahren nennen, weil es die Proportionalität des Wachsens der Potenzen und ihrer Exponenten wenigstens in dem Bereich zwischen den beiden Exponenten 31 und 32 vorausgesetzt hat; das Proportionalverfahren ist auf der rechnerischen Seite das Gleiche, was auf der zeichnerischen Seite das Voraussetzen der Geradlinigkeit der Kurve ist.
Mit Hilfe dieses Verfahrens könnten wir nun auch die nächsten Lücke, die in der Potenzreihe zwischen 4 und8 liegt, schließen, indem wir log 5, log 6 und log 7 berechnen, und dann alle folgenden Lücken behandeln, ganz abgesehen davon, dass es jedesmal um eine mühselige Rechnung handelt, die nicht einmal zu hinreichend genauen Werten führt. Erleichternd würde bei der ganzen Arbeit wirken, dass wir nur die Logarithmen der sogenannten Primzahlen zu berechnen brauchen, d.h. log 3, log 5, log 7, log 11, log 13 usw. Die Logarithmen aller anderen Zahlen sind ja aus denjenigen der Primzahlen auf einfache Srt zu ermitteln. Z.B. ist:

7. Gebrochene Exponenten

Bisher haben wir zu den Lückenzahlen unserer Potenzreihe die zugehörigen Exponenten ermittelt. Man könnte auch den anderen Weg einschlagen, dass man zuerst in der Exponentenreihe Einschaltungen vornimmt und alsdann die zugehörigen Potenzzahlen zu ermitteln sucht. Zum Beispiel werde zwischen dei Exponenten 0 (Null) und 1 der Exponent ½ eingeschaltet. 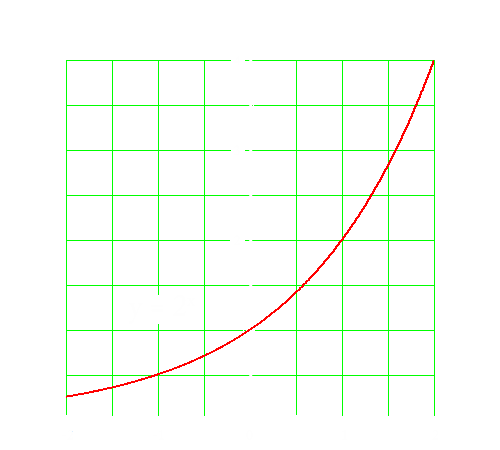Welche Potenzzahl gehört zu ihr? Rein formal gehört zu ihr die Potenz 2^½. Was ist unter ihr zu verstehen? Diese Frage tauchte schon einmal früher auf, als wir uns mit der Kurve y = 2^x beschäftigten. In der Grafik rechts ist diese Kurve für einen kleinen Wertebereich noch einmal exakt dargestellt. Als Material zur Zeichnung jener Kurve standen uns damals nur solche Potenzen der Basis 2 zur Verfügung, deren Exponent eine positive oder negative ganze Zahl einschließlich der Null ist. Wie steht es um solche Potenzen der Basis 2, deren Exponent eine gebrochene Zahl ist, z.B. um die Potenz 2^½?
Diese Frage lässt sich nunmehr durch die Regel beantworten, die wir als die letzte der vier Vereinfachungsregeln gewannen:
Eine Potenz wird radiziert, indem man ihren Exponenten durch den Exponenten der Wurzel dividiert.
Wir fanden dort beispielsweise, dass ³√(2⁶) = 2^{6 : 3} = 2² ist. Gäbe es eine Wurzel von der Form ²√(2¹), so müsste sie nach dieser Regel in die Potenz

umgeschrieben werden können. Dem Sinne der Potenz 2^½ auf die Spur zu kommen, ist daher gleichbedeutend damit, dass man der Wurzel ²√(2¹) einen Sinne zu geben vermag. Da 2¹ die Zahl 2 selber ist, handelt es sich also um die Untersuchung der Wurzel

8. Dekadische Logarithmen

Nun ist das Reihenpaar reif gemacht, zur Ausführung von Multiplikationen, Divisionen, Potenzierungen und Radizierungen verwendet zu werden. Bisher haben wir uns dabei auf ein Reihenpaar beschränkt, das auf der Zahl 2 als Basis ruht. Es hätte natürlich auch eine andere Zahl als Basis genommen werden können. Bei der Erfindung der Logarithmen durch Bürgi und Neper bildeten auch andere Zahlen die Grundlage, Zahlen, die dort auf den ersten Blick gar nicht einmal hervortreten und, wenn man sie ans Licht zieht, verhältnismäßig kompliziert erscheinen; bei Bürgi war es die Zahl 1,0001, bei Neper die Zahl 0,9999999.
Als 1614 Neper's Werk erschien, fand es einen glühenden Bewunderer in Professor Henry Briggs. Bei einer Zusammenkunft beider im Jahre 1615 schlug Briggs als Basis die Zahl 1/10 vor. Neper ergänzte den Vorschlag dahin, dann doch lieber die Zahl 10 zu wählen, wobei es dann auch blieb. Briggs machte sich nun mit Feuereifer unter Mitarbeit von acht Gehilfen an das Riesenwerk der Berechnung dieser "dekadischen" Logarithmen, die heute ihm zu Ehren auch Brigg'sche Logarithmen genannt werden, und gab bereits im Jahre 1617 seine "Logarithmorum Chilias prima" (der Logarithmen erstes Tausend) heraus; sie enthielt die dekadischen Logarithmen der Nummer 1 bis 1000 bis auf 8 Stellen nach dem Komma, sogenannte 8stelligen Logarithmen. Im Jahre 1624 ließ er seine "Arithmetica logarithmica" erscheinen, die für die Nummer 1 bis 20 000 und 90 000 bis 100 000 sogar 14stellige Logarithmen lieferte.
Der Grund, warum die Basis 10 anderen Grundzahlen verdrängte, liegt auf der Hand. Denn die Ordnung unseres Zahlensystems beruht auf der Zahl 10 und ihre Potenzen, d.h. auf der Potenzreihe:

Potenzen		⋅⋅⋅⋅⋅		10-3		10-2		10-1		100		101		102		103		104		⋅⋅⋅⋅⋅		oder
		⋅⋅⋅⋅⋅		1/1000		1/100		1/10		1		10		100		1000		10 000		⋅⋅⋅⋅⋅		oder
		⋅⋅⋅⋅⋅		0,001		0,01		0,1		1		10		100		1000		10 000		⋅⋅⋅⋅⋅
Exponenten		⋅⋅⋅⋅⋅		-3		-2		-1		0		1		2		3		4		⋅⋅⋅⋅⋅

Indem wir etwa die Zahl 386,24 hinschreiben, fügen wir Vielfache der einzelnen Zehnerpotenzen zusammen:

386,24

=

3 ⋅ 100

+

8 ⋅ 10

+

6 ⋅ 1

+

2 ⋅ 0,1

+

4 ⋅ 0,01

Es lässt sich also vermuten, dass in bezug auf die so geschriebenen Zahlen ein Logarithmensystem auf der gleichen Basis besondere Einfachheiten hervortreten lässt.
Welcher Art diese Einfachheiten sind, zeigt bereits das obige Reihenpaar: der Exponent ist stets gleich der Anzahl der Nullen ihres Numerus. Was wird aus dieser Nullengesetzmäßigkeit, wenn in dem entsprechenden Reihenpaar, um es praktisch verwertbar zu machen, die Lücken ausgefüllt werden? Dieses Reihenpaar hieß ja:

Numeri		⋅⋅⋅⋅⋅		0,001		0,01		0,1		1		10		100		1000		10 000		⋅⋅⋅⋅⋅
dekadischer Logarithmus		⋅⋅⋅⋅⋅		-3		-2		-1		0		1		2		3		4		⋅⋅⋅⋅⋅

Die erste Lücke rechts der 1 in der Numerireihe ist die zwischen 1 und 10; in der Logarithmusreihe entspricht ihr die Lücke zwischen 0 (Null) und 1. Mithin wissen wir:

log 2		=		0,⋅⋅⋅⋅
log 3		=		0,⋅⋅⋅⋅
log 4		=		0,⋅⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
log 9		=		0,⋅⋅⋅⋅

Man sagt, alle diese Logarithmen haben die Kennziffer oder Charakteristik 0 (Null), und meint damit den Bestandteil vor dem Komma. Halten wir fest, dass alle einstelligen Numeri (1, 2, 3, 4, 5, 6, 7, 8, 9) einen Logarithmus mit der Kennziffer 0 (Null) besitzen! Der Bestandteil des Logarithmus nach dem Komma pflegt Zugabe oder Mantisse (vom lateinischen mantissa) genannt zu werden. Beschränken wir uns für die Mantisse auf vier Dezimalstellen, so ergibt sich etwa auf Grund einer Rechnung, wie wir sie für log 3 auf der Basis 2 andeuteten:

log 2		=		0,3010
log 3		=		0,4771
log 7		=		0,7782

Die übrigen Logarithmen ergeben sich auf Grund der Vereinfachungsregeln:

log 4

=

log (22)

=

2 ⋅ log 2

=

0,6021

log 5

=

log (10 : 2)

=

log 10 - log 2

=

1 - log 2

=

0,6990

log 6

=

log (2 ⋅ 3)

=

log 2 + log 3

=

0,7782

log 8

=

log (23)

=

3 ⋅ log 2

=

0,9031

log 9

=

log (32)

=

2 ⋅ log 3

=

0,9542

Es könnte auffallen, dass z.B. log 4 = 2 ⋅ log 2 = 2 ⋅ 0,3010 als 0,6021 und nicht als 0,6020 herauskommt. Das rührt davon her, dass in den 4stelligen Logarithmen ja Abrundungen vorliegen. 5stellig ist

log 2		=		0,30103
log 4		=		0,60206

Daraus entsteht eben durch Abrundung auf 4 Stellen:

log 2		=		0,3010
log 4		=		0,6021

Wir gehen an die zweite Lücke rechts der 1 in der Numerusreihe. Sie liegt zwischen 10 und 100; in der Logarithmenreihe entspricht ihr die Lücke zwischen 1 und 2. Mithin wissen wir bereits:

log 11		=		1,⋅⋅⋅⋅
log 12		=		1,⋅⋅⋅⋅
log 13		=		1,⋅⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
log 99		=		1,⋅⋅⋅⋅

Wir sehen, alle diese zweistelligen Numeri haben einen Logarithmus mit der Kennziffer 1. Die Mantissenbestimmung braucht wieder nur für die Primzahlen zwischen 10 und 100 direkt vorgenommen zu werden. Dabei stehen die Mantissen der reinen Zehner, also 20, 30, 40, ⋅⋅⋅⋅ 90, von der ersten Lücke her bereits fest:

log 20

=

log (2 ⋅ 10)

=

log 2 + log 10

=

0,3010 +1

=

1,3010

log 30

=

log (3 ⋅ 10)

=

log 3 + log 10

=

0,4771 +1

=

1,4771

⋅⋅⋅

⋅⋅⋅

Ganz allgemein gilt, dass eine Anhängung von Nullen an einen Numerus in dessen Logarithmus nur die Kennziffer ändert; die Mantisse bleibt davon unberührt.
Für die weiteren Lücken rechtes der 1 in der Numerusreihe ergeben sich, wie sofort ersichtlich ist, folgende Kennzifferbestimmung:

3stellige Numeri				Kennziffer des Logarithmus ist 2
4stellige Numeri				Kennziffer des Logarithmus ist 3
5stellige Numeri				Kennziffer des Logarithmus ist 4
⋅⋅⋅
⋅⋅⋅

Allgemein:

Der Logarithmus eines n-stelligen Numerus hat die Kennziffer n-1.

Wir wollen nunmehr aus Gründen, die sich uns sogleich ergeben werden, prinzipiell alle Ligarithmen so schreiben, dass sie mit der 0,⋅⋅⋅⋅ beginnen, und dass ihre Kennziffer hinter der Mantisse zugefügt wird. Wir schreiben also nicht mehr:

log 20

=

1,3010

sondern

log 20

=

0,3010 + 1

Dann bekommt die obige "Kennzifferregel" die Gestalt:

Der Logarithmus eines n-stelligen Numerus hat die Form 0,⋅⋅⋅⋅ + (n - 1).

Es obliegt uns noch, uns über die Logarithmen solcher Numeri zu orientieren, die selber mit einem Komma behaftet sind, womit dann auch die Lücken links der 1 in der Numerusreihe und die entsprechenden Lücken in der Logarithmenreihe geschlossen würden. An einem konkreten Beispiel erkennt man hier am besten, wie es sich verhält. Greifen wir etwa log 113 heraus! Wir wollen im Numerus eine Stelle nach der anderen abstreichen und sehen, was sich dadurch im Logarithmus verändert.

log 113

=

0,0531 + 2

ist also die Gegebenheit, auf der wir aufbauen.

1)

log 11,3

=

log (113 : 10)

=

log 113 - log 10

=

(0,0531 + 2) - 1

=

0,0531 + 1

2)

log 1,13

=

log (113 : 100)

=

log 113 - log 100

=

(0,0531 + 2) - 2

=

0,0531 + 0

3)

log 0,113

=

log (113 : 1000)

=

log 113 - log 1000

=

(0,0531 + 2) - 3

=

0,0531 - 1

⋅⋅⋅

⋅⋅⋅

Oder etwas übersichtlicher:

Zusammenstellung:				Numerus				Logarithmus
log 113 = 0,0531 + 2				3/stellig				0,⋅⋅⋅⋅ + 2
log 11,3 = 0,0531 + 1				2/stellig				0,⋅⋅⋅⋅ + 1
log 1,13 = 0,0531 + 0				1/stellig				0,⋅⋅⋅⋅ + 0
log 0,113 = 0,0531 - 1				null/stellig				0,⋅⋅⋅⋅ - 1
log 0,0113 = 0,0531 - 2				- 1/stellig				0,⋅⋅⋅⋅ - 2
log 0,00113 = 0,0531 - 3				- 2/stellig				0,⋅⋅⋅⋅ - 3
log 0,000113 = 0,0531 - 4				- 3/stellig				0,⋅⋅⋅⋅ - 4
⋅⋅⋅
⋅⋅⋅

Diese Übersicht zeigt uns, dass die Regel:

Der Logarithmus eines n/stelligen Numerus hat die Form 0,⋅⋅⋅⋅ + (n - 1).

ganz allgemeine Gültigkeit besitzt. Man muss nur mit dem Begriff der Stelligkeit des Numerus geschickt umgehen können. Weist der Numerus kein Komma auf, so ist seine Stelligkeit einfach die Anzahl seiner Ziffern. Weist der Numerus ein Komma auf, so sind zwei Fälle zu unterscheiden:

1. Fall:

Vor dem Komma stehen wirkliche Ziffern, also nicht bloß eine Null, so dass eine unechte Dezimalzahl vorliegt. Dann bestimmt die Anzahl der Ziffern vor dem Komma die Stelligkeit. So ist z.B. der Numerus 11,3 zweistellig.

2. Fall:

Vor dem Komma steht eine Null, so dass eine echte Dezimalzahl vorliegt. Dann bestimmt die Anzahl der Nullen, die sich unmittelbar nach dem Komma zwischen das Komma und die wirklichen Ziffern schieben, die Stelligkeit, und zwar wird diese Anzahl der Nullen negativ gerechnet. So hat z.B. 0,000113 die Stelligkeit -3, da zwischen dem Komma und der Zifferngruppe 113 drei Nullen stehen. Der Numerus 0,113 ist dagegen 0/stellig, da zwischen dem Komma und der Zifferngruppe keinerlei Null vorhanden ist. Die Null vor dem Komma wird nicht mitgezählt.

Man muss sich durch Übung in die Lage versetzen, die "Kennzifferregel" sicher vorwärts und rückwärts anwenden zu können. Ist etwa ein Logarithmus von der Form 0,⋅⋅⋅⋅ - 5 bekannt, so muss man wissen, dass sein Numerus 4/stellig ist, dass dieser also zwischen dem Komma und der Zifferngruppe 4 Nullen besitzt und vor dem Komma natürlich dann ebenfalls eine Null aufweist.
In den Lehrbüchern über elementare Mathematik ist es bei der Schilderung der dekadischen Logarithmen üblich geworden, statt einer einzigen Kennzifferregel, wie sie hier aufgestellt ist, deren zwei zu formulieren. Man unterscheidet dabei die Numeri, die mit 0,⋅⋅⋅⋅ beginnen, von denjenigen, welche anders beginnen. Für die erstere formuliert man die Kennzifferregel etwa folgendermaßen:

Fängt der Numerus mit 0,⋅⋅⋅⋅ an, so fängt auch der Logarithmus mit 0,⋅⋅⋅⋅ an, und hinten ist noch die Anzahl der Nullen des Numerus abzuziehen.

So ist beispielsweise log 0,000113 = 0,⋅⋅⋅⋅ - 4.

Für die Numeri, die anders beginnen, wird die von uns aufgestellte einzige Kennzifferregel in der Form verwendet:

Der Logarithmus eines n-stelligen Numerus hat die Kennziffer n - 1.

So ist beispielsweise log 11,3 = 1,⋅⋅⋅⋅, weil der Numerus 2/stellig ist. Aber es ist nicht nötig, das Kennziffergesetz in zwei Regeln aufzuspalten. Man kommt mit einer einzigen Regel aus, wenn man den Begriff der Stelligkeit des Numerus auf alle Numeri, also auch auf diejenigen ausdehnt, welche mit 0,⋅⋅⋅⋅ beginnen, und wenn man ferner ein für alle Male den Logarithmus mit 0,⋅⋅⋅⋅ beginnen lässt und erst hinter der Mantisse die Kennziffer hinzufügt! Diese wähle man dann nach unserer Kennzifferregel der Stelligkeit des Numerus entsprechend.
Bei Verwendung zweier Kennzifferregeln, die noch dazu vorwärts und rückwärts beherrscht werden müssen, ist endlosen Verwechselungen und mannigfachen Irrtümern Tür und Tor geöffnet, denen der Anfänger kaum auszuweichen vermag.

9. Handhabung der Logarithmentabelle

Auszug aus: Richard Feynman, "Sie belieben wohl zu scherzen, Mr. Feynman" - Abenteuer eines neugierigen Physikers, Piper- Verlag, 1987:

»Als ich in Los Alamos war, stellte ich fest, daß Hans Bethe im Rechnen absolut Spitze war. Einmal zum Beispiel schrieben wir ein paar Zahlen in eine Formel und kamen zu 48 zum Quadrat. Ich lange nach der Marchant-Rechenmaschine, und er sagt: "Das ist 2300." Ich fange an, auf die Knöpfe zu drücken, und er sagt: "Wenn du's genau wissen willst, es ist 2304."
Die Maschine zeigte 2304 an. "Mensch! Is' ja toll!" sage ich.
"Weißt du nicht, wie man die Zahlen in der Nähe von 50 quadriert?" fragt er. "Du quadrierst 50 - das gibt 2500 -, und dann subtrahierst du 100mal die Differenz deiner Zahl von 50 (in diesem Fall 2), so hast du 2300. Wenn du die Korrektur machen willst, quadriere die Differenz und addiere das dazu. Das macht 2304."
Ein paar Minuten später müssen wir die Kubikwurzel von 2,5 ziehen. Um auf dem Marchant Kubikwurzeln zu ziehen, mußte man für die erste Näherung eine Tabelle verwenden. Ich öffne die Schublade, um die Tabelle herauszuholen - diesmal dauert es ein bißchen länger -, und er sagt: "Das ist ungefähr 1,35."
Ich rechne es auf dem Marchant nach, und es stimmt. "Wie hast du's denn diesmal gemacht?" frage ich. "Hast du irgendeine Zauberformel, wie man Kubikwurzeln zieht?"
"Oh", sagt er, "der Logarithmus von 2,5 ist soundso. Ein Drittel von diesem Logarithmus liegt zwischen den Logarithmen von 1,3, der soundsoviel ist, und 1,4, der soundsoviel ist, und da habe ich interpoliert."
Auf diese Weise fand ich etwas heraus: Erstens, er kennt die Logarithmentafel; zweitens, allein für die Rechenoperationen, die er angestellt hat, um die Interpolation zu machen, hätte ich länger gebraucht als es dauert, die Tafel herauszuholen und auf die Knöpfe der Rechenmaschine zu drücken. Ich war beeindruckt.«

Wir verstehen bereits, dass es in einer Logarithmentafel nicht nötig ist, die Kennziffer anzugeben. Es handelt sich darin nur um die Angabe der Mantissengruppe, die zu der Zifferngruppe des Numerus gehört. Um ein konkretes Beispiel einer "alten" Logarithmentafel vor uns zu haben, sei hier eine Seite der 1844 von Charles Babbage veröffentlichten Logarithmentafel gezeigt, das ganze Werk beinhaltet die Zahlen 1 bis 108000. Es zeigt sich, dass sie sich im Aufbau nicht nicht von unserer Referenztabelle unterscheidet. 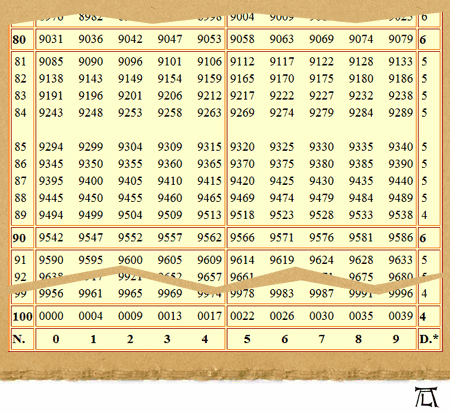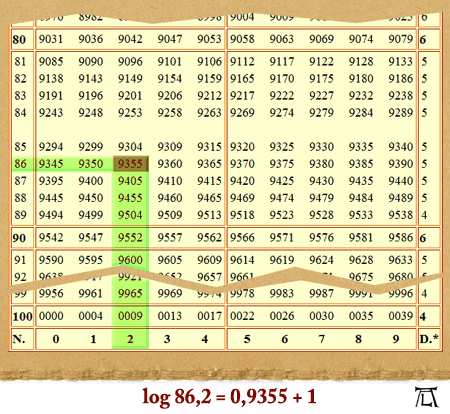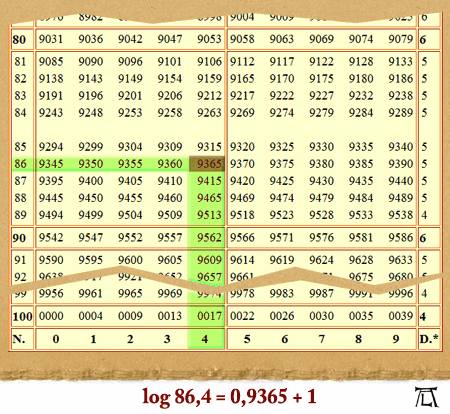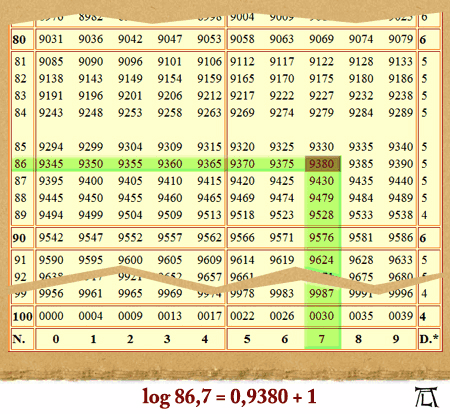Auch Babbage verwendete meist vierziffrige Mantissengruppen. Die Numeri sind jeweils links fortlaufend von oben nach unten angeordnet, und ganz rechts befindet sich eine Spalte, die die Differenz der letzen Mantissengruppe der jeweiligen Zeile zur ersten Mantissengruppe der nächsten Zeile anzeigt.
Nehmen wir z.B. den Numerus 86, wie in der Grafik links gezeigt. Auf den ersten Blick listet die 86er Zeile die Numeri 86,0, 86,1, 86,2, 86,3, ⋅⋅⋅⋅ auf, deren zugehörigen Mantissengruppen im Kreuzungspunkt der betreffenden Parallelzeile und Parallelspalte zu finden sind, also z.B.:

log 86,2		=		0,9355 + 1
log 86,4		=		0,9365 + 1		und
log 86,7		=		0,9380 + 1

Die (+ 1) hinter der Mantissengruppe deutet darauf hin, dass der Numerus 86 die Stelligkeit +2 besitzt.
Wir wissen jedoch bereits, dass die Mantissengruppe, also M, stets unverändert bleibt, und sich nur die Stelligkeit der Numeri ändern kann, dass also z.B.:

⋅⋅⋅⋅

=

M (0,862)

=

M (8,62)

=

M (86,2)

=

M (862)

=

M (8620)

=

⋅⋅⋅⋅

ist. In Wahrheit hat unsere Referenztabelle also eine Wertebereich von -∞ bis +∞!
Diese Einsicht ist zwar einerseits wunderbar und etwas verblüffend, rückt jedoch ein weiteres Problem in den Fokus unseres Interesses: Das Problem der Auf- und Abrundung von Zahlen.
Mantissenziffern, die mit einer 5 enden, sind besonders verdächtig, da sie meist unmittelbar danach entweder auf- oder abgerundet sein könnten. Einige Autoren und Mathematiker haben daher eine eigene Kennzeichnung der letzten 5 einer Mantissengruppe eingeführt. Wenn sie durch Aufrundung entstand, nannte man sie z.B "kleine Fünf" und kennzeichnete sie mit einem Überstrich, 5, eine durch Abrundung entstandene 5 bezeichnete man dementsprechend als "große Fünf", sie wurde z.B. mit einem Unterstrich gekennzeichnet: 5. So ist die fünfstelligen Mantisse von

log 854		eigentlich		93 146		und von
log 717		eigentlich		85 552

was zu einer vierstelligen Mantisse von

log 854		=		9315		(Aufrundung!)		und
log 717		=		8555		(Abrundung!)

führt. Wie wichtig eine solch Unterscheidung sein kann, sehen wir, wenn wir 854.000² ermitteln wollen. Die Differenz aufgrund der zwei verschiedenstelligen Mantissenwerte von

antilog [2 ⋅ (0,9315 + 5)]		=		7,2946 ⋅ 1011		und
antilog [2 ⋅ (0,93 146 + 5)]		=		7,2935 ⋅ 1011

ist immerhin 290.000.000! Der richtige Wert wäre übrigens 7,29316 ⋅ 10¹¹, aber das sei nur nebenbei erwähnt. Diese kleinen Rundungsfehler addieren, multiplizieren und potenzieren sich also je nach den folgenden Rechenoperationen mächtig auf. Aber diese Ab- und Aufrundung ist doch in allen vierstelligen Mantissen wirksam gewesen! Müsste man nicht also die letzte Ziffer jeder vierstelligen Mantisse unter- bzw. überstreichen? Zweifellos könnte man dies tun. Aber es ist unnötig im Hinblick auf den Zweck, den die alleinige Kennzeichnung der 5 verfolgt. Angenommen nämlich, wir wollten aus einer vierstelligen Mantisse eine dreistellige Mantisse hervorgehen lassen. Dann würde die letzte der vier Ziffern weggelassen und die vorletzte Ziffer eventuell um 1 erhöht werden müssen, nämlich dann, wenn die weggelassene Ziffer 6, 7, 8 oder 9 hieß. Im Falle, dass die letzte Ziffer eine 5 war, könnte man im Zweifel sein, ob die vorletzte Ziffer erhöht werden muss oder nicht; dieser Zweifel wird durch den Strich über oder unter der 5 behoben, da nur die große Fünf eine Erhöhung der vorletzten Ziffer bewirkt.
Einmal angenommen, wir wollen nun log 6774 bestimmen. Dieser Numerus liegt zwischen 6770 und 6780 eingeschaltet. Für diese Grenznumeri finden wir in unserer Referenztabelle folgende Mantissen:

log 6770		=		8306 + 3		und
log 6780		=		8312 + 3

Wir könnten unser bekanntes Proportionalverfahren anwenden. Dem Anwachsen des Numerus um 10 entspricht also ein Anwachsen der Mantisse um 6; man nennt diese 6 die Teildifferenz. Es bleibt nun bloß noch auszurechnen, um wieviel die Mantisse wächst, wenn der Numerus nicht um 10, sondern bloß um 4, nämlich von 6770 auf 6774, wächst. Wüchse der Numerus nicht um 10, sondern bloß um 1, so wüchse die Mantisse nicht um 6, sondern bloß um 0,6; also hat ein Anwachsen des Numerus um 4 ein Anwachsen der Mantisse um 4 ⋅ 0,6 = 2,4 zur Folge. Es kommt also zu der Mantisse 8306 der Zuwachs 2,4 hinzu. Da aber die Mantisse vierziffrig bleiben soll, muss man ihren Zuwachs 2,4, welchen man auch Proportionalteil (pars proportionalis, abgekürzt p.p.) nennt, auf 2 abrunden und erhält die Mantisse 8308, so dass man nun weiß:

log 6774

=

8308 + 3

Wie würde es nun mit log 13.734 aussehen? Unsere Referenztabelle liefert hierzu die Grenznumeri 1370 und 1380 und die dazu gehörigen Mantissen 1367 und 1399. Die Teildifferenz beträgt also 32. Für die 4. Numerusziffer 3 beträgt mithin der zu 1367 hinzukommende Proportionalteil 3 ⋅ 3,2 = 9,6, wogegen für die 5. Numerusziffer 4 der Proportionalteil 4 ⋅ 0,32 = 1,28 beträgt. Beide Proportionalteile zusammen betragen 10,88 und werden zu 1367 hinzugefügt. Wir runden auf und erhalten:

log 13.734

=

0,1378 + 4

Es kann aber auch der umgekehrte Fall eintreten, dass verlangt wird, zu einer Mantisse den Numerus aufzusuchen. Dann muss man in der Tafel den Weg vom Innern zum Rand hin nehmen. Falls die Mantisse abgedruckt ist, ist der Numerus am Rande leicht zu ermitteln. Wie aber, wenn die gegebene Mantisse nicht in der Tafel steht, sondern zwischen zwei in der Tafel angegebenen Mantissen liegt? Wieder soll uns ein Beispiel über den dann einzuschlagenen Weg orientieren:

log x

=

0,1155 + 2

Die Mantisse 1155 liegt in unserer Referenztabelle zwischen den beiden Mantissen 1139 und 1173. Also liegt der Numerus zwischen den zu diesen beiden Mantissen gehörigen Numeri, d.h. zwischen 130 und 131, wofür man ebensogut sagen kann: zwischen 1300 und 1310. Die Tafeldifferenz beträgt 34 (1173 - 1139 = 34); zu diesem Mantissenzuwachs gehört der Numeruszuwachs 10 (1310 - 1300 = 10). Der Proportionalteil beträgt aber nur 16 (1155 - 1139 = 16); ihm entspricht ein proportional geringerer Numeruszuwachs, der sich aus der Aufgabe ermittelt:

zum Mantissenzuwachs		34		gehört der Numeruszuwachs		10
zum Mantissenzuwachs		16		gehört der Numeruszuwachs		?

Es ist ohne weiteres klar, dass der gesuchte Numeruszuwachs 8/17 von 10 oder 4,71 ist. Unser Numerus heißt demnach 1300 + 4,71 = 1304,71. Die Kennziffer (+ 2) verrät uns, dass der Numerus dreistellig sein muss, so dass wir nun wissen:

x

=

130,471

Wenn also eine Mantisse nicht in der Tafel zu finden ist, weist dies darauf hin, dass der Numerus nicht bloß vier- sondern fünf- oder gar sechsziffrig ist; auf siebente, achte und folgende Ziffern des Numerus verzichten wir in einem solchen Fall, da wir mit ihnen doch nur zum Schein genau wären.

Nachdem wir uns so die Technik des Aufsuchens von Logarithmen und Numeri angeeignet haben, können wir auch die Sätze verstehen, die H.B. Lübsen über den Wert der Logarithmen in seinem mathematischen Unterrichtswerk um 1860 geschrieben hat:

"Erst als man an Logarithmen dachte und vollständige Tafeln für sie berechnete, wurde die praktische Arithmetik zur Vollkommenheit gebracht. Rechnungen, die noch zu Kepler's Zeiten ganze Tage und Wochen erforderten, oder die man gar, wegen unübersteigbarer praktischer Schwierigkeiten, zum großen Nachteil der Wissenschaft und des bürgerlichen Wohls ganz aufgeben mußte, können jetzt mit Hilfe der Logarithmen in wenigen Minuten selbst von einem Anfänger der Mathematik gemacht werden. Und nicht ganz unpassend sagt daher ein Engländer: die Logarithmen sind in der Mathematik das, was die Dampfmaschine in der Mechanik ist."

10. Das Verhältnis der verschiedenen Logarithmensysteme zueinander

Ziemlich zu Beginn unserer "Logarithmen-Saga" hatten wir wir das Reihenpaar

Potenzen		0		⋅⋅⋅⋅⋅		1/32		1/16		1/8		1/4		1/2		1		2		4		8		16		32		⋅⋅⋅⋅⋅		∞
Exponenten		- ∞		⋅⋅⋅⋅⋅		- 5		- 4		- 3		- 2		- 1		0		1		2		3		4		5		⋅⋅⋅⋅⋅		∞

verbildlicht, indem wir auf einer waagerechten Gerade in gleichen Abständen die Exponenten auftrugen und senkrecht dazu nach oben in dem für die Exponenten gewählten Maßstab die Potenzen. Wir wollen diese Zeichnung nun dahin vereinfachen, dass wir nur die waagerechte Gerade als Trager der Exponenten beibehalten, die Senkrechte jedoch fortlassen und statt ihrer eine Art Erinnerung an die Länge die betreffende Potenzzahl zu dem zugehörigen Exponenten hinzuschreiben. Dann entsteht folgendes Bild:
br>

a)

Wie ersichtlich, bezeichnen die unterhalb der Geraden befindlichen Zahlen die einzelnen Exponenten oder Logarithmen, die oberhalb der Geraden befindlichen Zahlen die betreffenden Potenzzzahken oder Numeri. Nun wollen eir uns mit einer einzigen Beschriftung begnügen, indem wir die Exponentenbezeichnung weglassen, Dann entsteht folgendes Bild:

Die Exponentenfolge ist nun verschwunden und mit ihr auch die Basis 2, auf der sich alles aufgebaut hat. Es scheint zwar so, als ob die Beschriftung die Basis 2 zur Voraussetzung habe. Aber nichts hindert uns anzunehmen, dass für die Beschriftung die Basis 4 oder gar die Basis 8 bestimmend gewesen sei; dann hätte die Gerade vor dem Weglassen der Exponenten folgendes Aussehen haben müssen:

b)		Basis 4
c)		Basis 8

Wir nehmen die Basis 4 bzw. 8, wie es auch sein muss, über dem Exponenten 1 wahr. Über dem Exponenten 2 steht die zweite Potenz der Basis, nämlich 4 ⋅ 4 = 16 bzw. 8 ⋅8 = 64, usw. Wie steht es jedoch mit den Zwischenzahlen, unter denen nun keine Exponenten mehr zu finden sind? Betrachten wir doch einmal in der ersten der beiden Geraden (Basis 4!) die Mitte zwischen den beiden Exponenten 0 (Null) und 1! Dort hätte der Exponent ½ zu stehen; darüber finden wir die Potenz 2. Wenn diese Zuordnung richtig wäre, müsste gelten:

4½

=

2

Das ist auch richtig; denn unter der Potenz 4^½ versteht man die Wurzel ²√(4¹) = ²√4, d.h. diejenige Zahl, welche, mit sich selbst malgenommen, 4 ergibt, und da ist ja die Zahl 2. So könnte man in jedem einzelnen Falle zeigen, dass auch die Zwischenzahlen an richtiger Stelle stehen, wenn man statt der 2 eine andere Basis, etwa die 4 oder die 8, maßgebend sein lässt.
Wir kehren nun zu der Geraden, an welcher die Exponenten unbezeichnet geblieben sind zurück:

Von einer bestimmten Basis kann man also an ihr nicht mehr reden. Darum kann man an ihr den Exponenten 1 an jede beliebige Stelle setzen. Diese Stelle wird dann die Basis sein müssen. Welche Basis wir jedoch auch wählen mögen, zu ihr gehört stets der Exponent 0 (Null). Die nullte Potenz von jeder Basis hat eben, wie wir wissen, den Wert 1.
Ist nicht durch das Weglassen der Exponenten und das damit verbundene Verschwinden der Basis auch Sinn und Bedeutung der Geraden verloren gegangen? Was hat an ihr die Folge der Numeri 1, 2, 4, 8, ⋅⋅⋅⋅⋅ noch zu bedeuten? Das lässt sich nur dadurch ermitteln, dass man verschiedene Basen unterlegt und das dann Gemeinsame herausfindet. Wir hatten ja schon die Basen 2, 4 und 8 als Beispiele gewählt.

Basis 2 (siehe Gerade a!)
Wir betrachten die Entfernung vom Numerus 1 bis zu irgendeinem anderen Numerus, etwa bis zum Numerus 64. Diese Entfernung beträgt 6 Einheiten, d.h. so viel Einheiten, wie der zum Numerus 64 gehörige Logarithmus beträgt:



Entfernung vom Numerus 1 bis zum Numerus 64 gleich 6

=

log 64.

Basis 4 (siehe Gerade b!)
Wir betrachten wieder die Entfernung vom Numerus 1 bis zum Numerus 64. Sie beträgt jetzt 3 Einheiten, wobei die Einheit doppelt so groß wie die vorige ist. Wieder sind es so viel Einheiten, wie der zum Numerus 64 gehörige Logarithmus beträgt:



Entfernung vom Numerus 1 bis zum Numerus 64 gleich 3

=

log 64.

Basis 8 (siehe Gerade c!)
Wir fassen noch einmal die Entfernung vom Numerus 1 bis zum Numerus 64 ins Auge. Sie benötigt jetzt 2 Einheiten, wobei die Einheit dreimal so groß ist wie beim ersten Mal. Wieder sind es so viel Einheiten, wie der zum Numerus 64 gehörige Logarithmus beträgt:



Entfernung vom Numerus 1 bis zum Numerus 64 gleich 2

=

log 64.

Wir wollen die Stelle des Numerus 1 den ausgezeichneten Punkt der Gerade nennen. Dann haben wir für den Numerus 64 gefunden:

Die Entfernung des ausgezeichneten Punktes von dem Numerus 64 ist der Logarithmus von 64 in bezug auf diejenige Basis, die für die Maßeinheit bestimmend war.

Was für den Numerus 64 gezeigt wurde, lässt sich auch für jeden anderen Numerus zeigen, und die Beschränkung auf die Basen 2, 4 und 8 ist ebenfalls unnötig. Allgemein gilt:

Die Entfernungen des ausgezeichneten Punktes von den einzelnen Zahlen sind die Logarithmen der betreffenden Zahlen auf beliebiger, aber für alle Zahlen gleicher Basis.

Um nun auch noch den Schein, als ob die an der Geraden vorausgesetzte Basis die Zahl 2 gewesen wäre, zu zerstören, wollen wir alle möglichen ganze Zahlen, die an der Geraden rechts der 1 noch fehlen, sowie die entsprechenden Stammbrüche links der 1 einschalten, also zwischen 2 und 4 die Zahl 3, zwischen 4 und 8 die Zahlen 5, 6 und 7 usw. Es kommt natürlich darauf an, dass sie an die richtige Stelle der Geraden gesetzt werden. Eines ist dabei bereits klar, dass die Abstände zwischen den Zahlen 1, 2, 3, 4, 5, ⋅⋅⋅⋅⋅ nacht rechts zu immer kleiner werden; die Zahlen stehen immer dichter beieinander. Um ihre genaue Lage zu ermitteln, können wir nach dem Vorigen eine beliebige Basis zugrundelegen, auch die Basis 10, indem wir dann die Länge von 1 bis 2, von 1 bis 3, von 1 bis 4, von 1 bis 5 usw. als die dekadischen Logarithmen von 1, 2, 3, 4, 5, ⋅⋅⋅⋅⋅ aus unserer Referenztabelle entnehmen. Da wir die Maßeinheit, die wir zugrundelegen, noch frei haben, wollen wir der Strecke von 1 bis 10, also log 1,0000, die Länge 10 cm geben. Dann liegt der Zeichnung der Geraden folgende Aufstellung zugrunde:

Länge von

1 bis 2

=

log 2

=

0,3010

=

3,010

cm

" "

1 bis 3

=

log 3

=

0,4771

=

4,771

cm

" "

1 bis 4

=

log 4

=

0,6021

=

6,021

cm

" "

1 bis 5

=

log 5

=

0,6990

=

6,990

cm

" "

1 bis 6

=

log 6

=

0,7782

=

7,782

cm

" "

1 bis 7

=

log 7

=

0,8451

=

8,451

cm

" "

1 bis 8

=

log 8

=

0,9031

=

9,031

cm

" "

1 bis 9

=

log 9

=

0,9542

=

9,542

cm

" "

1 bis 10

=

log 10

=

1,0000

=

10,000

cm

Die Zahlen links der 1 ergeben sich dann auf Grund der Beziehungen:

log 0,9		=		0,9542 - 1		=		(9,542 - 10)	cm
log 0,8		=		0,9031 - 1		=		(9,031 - 10)	cm
log 0,7		=		0,8451 - 1		=		(8,451 - 10)	cm
⋅⋅⋅
⋅⋅⋅
log 0,2		=		0,3010 - 1		=		(3,010 - 10)	cm

Wir brauchen also von den Stellen 1, 2, 3, 4, 5, ⋅⋅⋅⋅⋅ nur um die Maßeinheit 10 cm nach links zu gehen, um auf die Stellen 0,1, 0,2, 0,3, 0,4, 0,5 ⋅⋅⋅⋅⋅ zu stoßen:

Ein Fortschreiten von den Stellen 1, 2, 3, 4, 5, ⋅⋅⋅⋅⋅ aus um die Länge der Maßeinheit 10 cm nach rechts hin würde zu den Zahlen 20, 30, 40, 50, ⋅⋅⋅⋅⋅ 100 führen. Ebenso falsch, wie es vorhin war, als Basis die Zahl 2 zu vermuten, würde es jetzt sein, als Basis dieser Einteilung die Zahl 10 zu vermuten, wenn auch bei der Herstellung der Einteilung die Basis 10 verwendet wurde. Aber nun, nachdem die Einteilung einmal da ist, kann ihr jede beliebige Basis zugrundeliegend gedacht werden. Wird die Basis 2 vorausgesetzt, so ist eben die Länge von 1 bis 2 die Einheit. Wird die Basis 10 vorausgesetzt, so ist die Länge 1 bis 10 die Einheit. Das heißt: Der Exponent 1 gehört das erste Mal unter die 2, das zweite Mal unter die 10.
Aus allem dem lässt sich eine interessante Schlussfolgerung ziehen, die sich vielleicht dem Leser schon von selber aufgedrängt hat. Vergleichen wir z.B. die horizontalen Längen für die Logarithmen auf der Basis 2, die man ja auch dyadische Logarithmen nennt, mit den horizontalen Längen für die Logarithmen auf der Basis 10, also für die dekadischen Logarithmen!

dyad. log 2

=

1

dek. log 2

=

0,3010

=

1 ⋅ 0,3010

dyad. log 4

=

2

dek. log 4

=

0,6021

=

2 ⋅ 0,3010

dyad. log 8

=

3

dek. log 8

=

0,9031

=

3 ⋅ 0,3010

⋅⋅⋅

⋅⋅⋅

Wir sehen, der dyadische Logarithmus einer Zahl z verhält sich zum dekadischen Logarithmus derselben Zahl z stets so, wie sich die Zahl 1 zur Zahl 0,3010 verhält. Nun ist 1 der dyadische Logarithmus von 2 und 0,3010 der dekadische Logarithmus von 2. Es gilt also die Proportion:

dyad. log z   dek. log z

=

dyad. log 2   dek. log 2

=

1 0,3010

Für jede Proportion ist ja das Produkt der Außenglieder gleich dem Produkt der Innenglieder; das heißt in unserem Fall:

1 ⋅ dek. log z

=

0,3010 ⋅ dyad. log z

Angenommen, man hätte nicht eine Tafel dekadischer, sondern eine solche dyadischer Logarithmen errechnet, und man wollte nun noch eine Tafel dekadischer Logarithmen gewinnen, so brauchte man also nur jeden dyadischen Logarithmus mit der Zahl 0,3010 zu multiplizieren, um den dekadischen Logarithmus desselben Numerus zu haben. Von größerer praktischer Bedeutung ist jedoch die umgekehrte Aufgabe:

aus dem vorhandenen dekadischen Logarithmensystem das dyadische zu errechnen!

Der Lösung dieser Aufgabe liegt dann die aus dem Obigen folgende Rechenbeziehung zugrunde:

dyad. log z		=		1/0,3010 ⋅ dek. log z
		=		3,3219 ⋅ dek. log z

Man nehme also alle dekadischen Logarithmen mit der Zahl 3,3219 mal, und man hat die dyadischen Logarithmen desselben Numerus.
Von einem Logarithmensystem zum anderen waltet also eine Übergangszahl, die man in der Mathematik den Modul nennt. Der Modul des dyadischen Systems in bezug auf das dekadische ist also die Zahl 3,3219⋅⋅⋅, wogegen der Modul des dekadischen Systems in bezug auf das dyadische die Zahl 0,3010⋅⋅⋅ ist. Die beiden genannten Module ergeben, wie wir gesehen haben, miteinander multipliziert, die Zahl 1; der eine ist, wie man sich auszudrücken pflegt, der reziproke Wert des anderen.
Welche logarithmische Bedeutung haben die beiden genannten Module? Von der einen Modulzahl, der Zahl 0,3010⋅⋅⋅, wissen wir bereits, dass sie der dekadische Logarithmus von 2 ist. Ist der andere Modul, due Zahl 3,3219⋅⋅⋅, auch ein Logarithmus? Um das zu unterscheiden, wenden wir die Proportionen

dyad. log z   dek. log z

=

dyad. log 2   dek. log 2

auf den Fall z = 10 an:

dyad. log 10   dek. log 10

=

dyad. log 2   dek. log 2

Nun wissen wir jedoch:

dek. log 10		=		1		und
dyad. log 2		=		1

Daher vereinfacht sich die letzte Proportion zu:

dyad. log 10

:

1

=

1

:

dek. log 2

Aus ihr gewinnen wir die Gleichung der Produkte der Außenglieder und der Innenglieder:

dyad. log 10

⋅

dek. log 2

=

1

Die Gleichung

3,3219

⋅

0,3010

=

1

ist damit identisch, und wir erkennen, dass die andere Modulzahl, nämlich 3,3219⋅⋅⋅, der dyadische Logarithmus der Zahl 10 ist.
Wir haben damit die beiden folgenden Übergangsformeln gefunden:

dek. log z

=

dek. log 2

⋅

dyad. log z

=

0,3010

⋅

dyad. log z

und

dyad. log z

=

dyad. log 10

⋅

dek. log z

=

3,3219

⋅

dek. log z

Was hier über das Verhältnis des dyadischen Systems zum dekadischen auseinandergesetzt worden ist, gilt natürlich auch für das Verhältnis zweier beliebiger Systeme zueinander; immer führt eine für die beiden feststehende Zahl, der Modul, von einem System zum anderen hinüber.

Was ist nun der Modul unseres "mayaischen" Logarithmensystems in bezug zum dekadischen? Wir erinnern uns: bei der Einführung des dekadischen Logarithmensystems in Abschnitt 8 hatte wir, in einem Link versteckt, das Zahlensystem der Maya vorgestellt. Die Zivilisation der Maya, die es seit etwa 2000 vor Chr. gab und die zwischen 250 und 900 ihre Blütezeit in Südamerika erlebte, benutzte als Basis ihres Zahlen- und somit Rechensystems die Zahl 20. In der folgenden Tabelle sind die Zahlen 0 bis 29 in der Mayaschreibweise dargestellt:

0	1	2	3	4	5	6	7	8	9
10	11	12	13	14	15	16	17	18	19
20	21	22	23	24	25	26	27	28	29

Für die 1 malten sie einen Punkt auf, für die 5 einen waagerechten Balken und sie kombinierten diese Zeichen, um die Zahlen 1 bis 19 zu schreiben. Seit dem Jahr 36 benutzten sie ein merkwürdiges ovales Zeichen für die 0 (Null). Dann stapelten sie diese 20 Ziffern übereinander, um die aufeinanderfolgenden Stellen ihres 20er-Systems zu kennzeichnen. Wir bleiben hier bei unserer gewohnten, horizontalen Ausrichtung der Ziffernabfolge.
Bei ihnen würden also die Ziffern 5-2-14, oder ,

5 ⋅ 20 ⋅ 20

+

2 ⋅ 20

+

14 ⋅ 1

=

2054

in unserer Schreibweise bedeuten. In unserer Referenztabelle finden wir nun:

dek. log 20

=

3010 + 1

Wir wissen ferner:

maya. log 20

=

1

Was ist nun z.B. der mayaische Logarithmus von 10? Eine Übergangsformel liefert uns das Verhältnis:

dek. log z

=

dek. log 20

⋅

maya. log z

⇒

maya. log 10

=

dek. log 10   dek. log 20

=

0,7686

was "überraschenderweise" der reziproke Wert von 1,3010 ist, also der reziproke Wert des dekadischen Logarithmus von 20. Somit gilt für die Module:

dek. log z		=		1,3010		⋅		maya. log z		und
maya. log z		=		0,7686		⋅		dek. log z

Der mayaische Logarithmus von wäre demnach:

maya. log

=

0,7686

⋅

dek. log 2054

=

5461 + 2

Wir bekommen hier ein, auf dem ersten Blick, verblüffendes Ergebnis: Die Kennziffer des Logarithmus ist (+ 2) und unsere Kennzifferregel, der Logarithmus eines n-stelligen Numerus hat die Form 0,···· + (n - 1), weist auf einen dreistelligen Numerus hin, 2054 ist jedoch vierstellig. Nun ist aber dreistellig! Unsere Kennzifferregel gilt also auch bei den alten Maya!
Ein weiteres erstaunliches Ergebnis erhalten wir, wenn wir den dekadischen Numerus von 5461 + 2 ermitteln. Die Mantissengruppe 5461 liegt in unserer Referenztabelle zwischen 5453 und 5465, welche zu den Numeri 351 und 352 gehören. Eine einfache Interpolation nach dem Proportionalverfahren liefert uns:

antilog 2,5461

=

351,6

Hätten wir anfangs blauäugig durch die simple Rechnung

5 ⋅ 10 ⋅ 10

+

2 ⋅ 10

+

14 ⋅ 1

=

500 + 20 + 14

=

534

in unser Zahlen- und Rechensystem übersetzt, wäre uns ein fataler Fehler unterlaufen! Davon hätte auch die Welt untergehen können ...

11. Der logarithmische Rechenschieber

Seitdem der Mensch Mathematik betreibt, benutzt er mechanische Hilfsmittel. In der gif-Graphik rechts sehe wir z.B. den assyrischen Sonnengott Shamash, der ein aufgewickeltes Seil und einen Messstab (Maßstab) in der rechten Hand hält, und den sumerischen König Ur-Nammu (2112 bis 2095 v. Chr.), der neben Seil und Ring anstatt des Maßstabes eine Messlatte in der rechten Hand hält - wahrscheinlich zur Landvermessung.
Eine interessante Randbemerkung wäre hier, dass der Stern in der Irakischen Flagge auf das assyrisch-babylonische Symbol für Shamash zurückgeht, das in diesem Relief dargestellt ist, und die assyrische Minderheit im Irak repräsentieren soll. Natürlich zeigt auch die Flagge der Assyrer selbst den Stern des Shamash!
Auch für die Logarithmen wurden bald nach den Tabellen mechanische Rechengeräte entwickelt, von kleinen, handlichen, vergleichbar mit unserem heutigen Taschenrechner, bis zu großen, komplexen, die Super-Computer des analogen, mechanischen Zeitalters. Diese Geräte wurden umworben wie das iPhone heute, wie das untere Bild zeigt. Doch wie funktionierten sie?
Wir wollen uns dazu zwei Holzstäbe denken, die aneinandergelegt, an ihren einanander zugekehrten Rändern die zuletzt mit Hilfe dekadischer Logarithmen gewonnenen Einteilung aufweisen. Mit dieser Kombination zweier gleichartiger Stäbe kann man wunderbar einfach Multiplikationen und Divisionen ausführen. Das wurde schon bald, nachdem Lord Neper die Logarithmen entdeckt hatte, von einem anderen Mathematiker erkannt. Im selben Jahr, in dem Briggs seine "Arithmetuka logarithmica" herausbrachte, im Jahre 1624 also, fertigte Edmund Gunter solche Rechenstäbe an; sie erhielten den Namen "Gunter's Scales", Seeleute nannten Gunter's Skala einfach nur "Gunter". Der Gunter war ziemlich groß, 2 Fuß, also 61 cm, lang und 1½ Inches, also etwa 40 mm, breit. Auf ihm waren neben den Werten von Sinus, Tangens oder auch der Loxodrome, eine Kurve auf einer Kugeloberfläche, die immer unter dem gleichen Winkel die Meridiane im Geographischen Koordinatensystem schneidet und daher auch Kursgleiche, Winkelgleiche oder Kurve konstanten Kurses genannt wird, auch die Werte des dekadischen Logarithmus eingraviert. Das nächsten Bild zeigt einen Gunter mit Sinus-, Tangens- und Logarithmusgravur.
Um ein einfaches Beispiel zu haben, wählen wir die Aufgabe 2 ⋅ 3. Zunächst mögen die zwei Gunter so nebeneinanderliegen, dass die gleichen Skalen und gleichen Zahlen übereinanderliegen. Nun schiebe man den unteren Gunter solange an dem oberen entlang, bis die untere 1 unter der oberen 2 erscheint. Dann werden wir über der unteren 3 auf dem oberen Gunter die Zahl entdecken, welche herauskommen muss, die 6. Der Grund dieses Verhaltens beider Gunter geht aus der für jede beliebige Basis geltende Vereinfachungsregel hervor:

log 6

=

log (2 ⋅ 3)

=

log 2 + log 3

Für die Division leuchtet uns nun die Handhabung des Gunterpaares bereits ein. Es handelt sich um die Aufgabe 6 : 3. Dann plaziert man den unteren Gunter so, dass die obere 6 über der unteren 3 erscheint. Über der unteren 1 wird dann das Ergebnis der Division, die 2, erscheinen. Hier liegt ja die Regel zugrunde:

log 2

=

log (6 : 3)

=

log 6 - log 3

Zwecks praktischer Handhabung verfeinerte man nun die Einteilung der beiden Gunter dadurch, dass man zwischen die ganzen Zahlen, da, wo es der Raum zulässt, Zehntel oder gar Hunderstel durch Unterteilungstriche einschaltete. Das gelingt natürlich nur, wenn man die Gunter hinreichend lang macht. Bei den käuflichen Guntern hat die Zahl 1 von der Zahl 10 etwa den Abstand 25 cm. Natürlich werden die Unterteilungen nach der Zahl 10 immer enger und, da man ja für das unbewaffnete Auge nicht beliebig dicht unterteilen kann, weil sonst beim Lesen alles verschwimmt, auch immer gröber. So kann der Raum zwischen 1 und 2 noch bis auf Hunderstel unterteilt werden, wobei zwischen zwei Hunderstelstrichen noch Abschätzungen möglich sind. Der Raum zwischen 9 und 10 ist jedoch bereits so eng, dass er nur in 20 Unterabteilungen gegliedert werden kann. Die Einteilung hat sich also von einem Ende zum anderen auf ein 5faches vergröbert.
Handelt es sich um Multiplikationen und Divisionen von Zahlen über 10, oder überschreitet das Ergebnis die Zahl 10, so kann man sich bei einem Gunterpaar, das nur bis 10 geht, dadurch helfen, dass man von den Zahlen, mit denen man zu operieren hat, Stellen solange abstreicht, bis sie selber und ihr Ergebnis unter 10 zu liegen kommen. So wird man statt der Aufgabe 1257 ⋅ 386 die Aufgabe 1,257 ⋅ 3,86 auf dem Gunterpaar rechnen und im abgelesenen Ergebnis, das 4,85 lautet, das Komma wieder um so viele Stellen nach rechts rücken, wie Stellen abgestrichen wurden, d.h. 5 Stellen, so dass 485.000 herauskommt. Eine direkte Multiplikation würde 485.202 ergeben haben. Aus dieser Technik ersehen wir, dass natürlich das Rechnen mit dem Schieber keine exakten Ergebnisse liefert; um der Schnelligkeit und Einfachheit der Rechnung willen muss man eben eine gewisse Ungenauigkeit in Kauf nehmen. Das Anwendungsgebiet des Rechenschiebers ist daher der Bereich derjenigen Rechnungen, bei denen über einen gewissen Grad der Genauigkeit nicht hinausgegangen zu werden braucht.
Um auch Potenzierungen oder gar Radizierungen vornehmen zu können, bedarf es einer weiteren Vervollkommnung des Apparates. Das Potenzieren ließe sich ja zur Not durch ein fortgesetztes Multiplizieren bewältigen. Aber schon beim einfachsten Radizieren, dem Berechnen einer zweiten Wurzel aus einer gegebenen Zahl, wäre man hilflos. Zum Zwecke des Arbeitens mit der zweiten Potenz und mit der zweiten Wurzel erfährt der Apparat die Ausstattung, die das nächste Bild zeigt.
Man kombinierte nicht zwei gleichartige Gunter miteinander, sondern einen Gunter, der von 1 bis 10 geht, und einen Gunter, der von 1 bis 100 geht, wobei die Distanz des zweiter Gunters zwischen 1 und 100 die gleiche ist wie die Distanz der Zahlen 1 bis 10 des ersten Gunters. Man macht also die Maßeinheit des zweiten Gunters nur halb so lang wie diejenige des ersten Gunters.
Zum Unterschiede gegen die beiden früheren, gleichartigen Gunter läßt man die beiden neuen Gunter fest miteinander verbunden in der Länge, wie es das Bild zeigt. Dann steht über jeder Zahl die Quadratzahl, ihre zweite Potenz; über der 2 sehen wir die 4, über der 3 die 9. Über der 4 würde die 16 zu stehen kommen, usw. Woher kommt das? Bei gleicher Maßeinheit beider Gunter müsste z.B. sein:

log 16

=

log 42

=

2 ⋅ log 4

Da aber die untere Maßeinheit das Doppelte der oberen ist wird log 16 oben ebenso lang wie log 4 unten. Während das Quadrieren auf einem Ermitteln der oberen Zahl auf Grund der unteren beruht, wird das Berechnen der zweiten Wurzel einer Zahl, das Quadratwurzelziehen, in umgekehrter Richtung vor sich gehen. Unter jeder Zahl steht ihre Quadratwurzel. In diesem Ermitteln der Quadratwurzel zeigt der Rechenschieber aufs eindeutigste seinen Nutzen.
Auch das Berechnen vierter Potenzen und vierter Wurzeln ist nun ein Leichtes, besteht doch das Erheben einer Zahl in die 4. Potenz in einem zweimaligen Quadrieren und das Berechnen der 4. Wurzel aus einer Zahl in dem Ermitteln der Quadratwurzel aus einer Quadratwurzel! Es handele sich z.B. um die Aufgabe ⁴√81! Wir suchen die Zahl 81 oben und finden unter ihr die 9, welche wir nun wiederum oben aufsuchen, um unter ihr die 3 zu finden; dann ist 3 die gesuchte 4. Wurzel.
Es bleibt nun noch zu überlegen, wie man in einem einzigen Apparate das Gunterpaar der Multiplikation und der Division mit dem Gunterpaar des Quadrierens und des Quadratwurzelziehens vereinigt. Die Lösung besteht darin, dass man bei dem letzeren Gunterpaar einen Zwischenraum nutenartig frei lässt, in den eine sogenannte Zunge eingeschoben wird. Dieselbe legt sich dann mit ihrem oberen Rande an den Gunter mit der Einteilung 1 - 100 an, mit ihrem unteren Rande an den Gunter mit der Einteilung 1 - 10. Man versieht nun die Zunge oben ebenfalls mit der Einteilung 1 - 100 und unten mit der Einteilung 1 - 10, so dass jetzt oben unmittelbar untereinander zwei kongruente Einteilungen 1 - 100 vorhanden sind und unten unmittelbar untereinander zwei kongruente Einteilungen 1 - 10. Bei herausgezogener Zunge sieht unser Apparat folgendermaßen aus:

Mit dieser Kombination von "Stab" und "Zunge" kann man mit Leichtigkeit sowohl multiplizieren wie dividieren wie quadrieren wie auch radizieren. Das Multiplizieren und Dividieren geschieht entweder längs der beiden unteren kongruenten Einteilungen 1 - 10 oder längs der beiden oberen konkruenten Einteilungen 1 - 100 durch Herausziehen der Zunge. Das Quadrieren und Quadratwurzelziehen bedarf ja der Zunge überhaupt nicht; diese wird dabei in den Stab völlig hineingeschoben.
Durch die Kombination von Stab und Zunge ist ein anderes Problem mitgelöst, nämlich das Berechnen der dritten Potenz und, was noch wichtiger ist, das Berechnen der Kubikwurzel, der dritten Wurzel!
Betrachten wir doch einmal die Aufgabe 4³. Bei eingeschobener Zunge steht über der unteren 4 des Stabes die obere 16 der Zunge, die aber nicht abgelesen zu werden braucht. Wir rücken nun die untere 1 der Zunge genau über diese untere 4 des Stabes. Über der oberen 4 der Zunge erkennen wir nun in der oberen Einteilung des Stabes die 64, was ja die 3. Potenz von 4 ist!
Wie geht es nun anders herum - mit z.B. der Aufgabe ³√64? Natürlich wissen wir durch Kopfrechnung, dass 4 herauskommen muss. Um dieses Ergebnis an unserem Apparat ablesen zu können, ziehen wir die Zunge ganz heraus und stecken sie verkehrt herum wieder hinein. Das folgende Bild zeigt die neue Konfiguration:

Die Einteilung 1 - 10 der Zunge ist nun oben, die 1 rechts, die 10 links, beide auf den Kopf gestellt. Die Einteilung 1 - 100 der Zunge wird nun unten liegen, die 1 rechts, die 100 links, beide ebenfalls auf den Kopf gestellt. Wir schieben nun die Zunge so weit nach links heraus, dass ihre obere 1 unter die 64 der obersten Einteilung zu liegen kommt. Dann werden auf den beiden oberen der vier Einteilungen lauter voneinander abweichende Zahlen untereinander stehen mit einer Ausnahme, die beiden Zahlen 4, die genau übereinander liegen wie in dem Bild gezeigt. Und diese 4 ist das gesuchte Ergebnis!
Übrigens stehen auch auf den beiden unteren der vier Einteilungen lauter voneinander abweichende Zahlen übereinander mit der Ausnahme wieder der Zahl 4, des gesuchten Ergebnisses. Woher kommt dies alles?
Um ³√64 zu erhalten, muss man nach der Vereinfachungsformel:

log 3√64

=

1/3 ⋅ log 64

die Strecke log 64, die sich oben von der der Zahl 1 bis zur Zahl 64 erstreckt, dritteln; am Ende des Drittels, das der Zahl 1 der obersten Einteilung rechts anliegt, wird die gesuchte Zahl ³√64 liegen müssen. Dieses Dritteln der Länge log 64 geschieht eben sinnvoll durch das verkehrte Hineinstecken der Zunge. Weil dabei die untere Einteilung der Zunge nach oben zu liegen kommt und weil diese Einteilung eine doppelt so große Maßeinheit wie die oberste Einteilung aufweist, ist die Strecke 1 bis 4 oben auf der verkehrten Zunge doppelt so lang wie die sich links an sie anlegende Länge von 4 nach 1 der obersten Einteilung, und die Länge von 1 nach 64 der obersten Einteilung ist tatsächlich an den beiden übereinanderstehenden Vieren gedrittelt.
Will man eine andere, nicht bereits im Kopf errechnete Kubikwurzel ziehen, etwa ³√20, so rücke man die obere 1 der verkehrten Zunge unter die 20 der obersten Einteilung. Wieder stehen auf den beiden oberen Einteilungen lauter verschiedene Zahlen untereinander mit einer Ausnahme, und diese Ausnahme ist das gesuchte Ergebnis. Es gehört allerdings schon einige Übung und Vertrautheit mit der Handhabung des Apparates dazu, um diese Ausnahme zu entdecken und abzulesen.
Um dies zu unterstreichen, zeigt das nächste Bild einen noch vor wenigen Jahren in jedem Schreibwarenladen erhältlichen Rechenschieber:

Um das genaue Ablesen untereinanderstehender Zahlen zu erleichtern, ist ein Fenster angebracht, das einen vertikalen Ätzstrich aufweist und sich längs des Gunterpaares verschieben lässt. Dies, einige Konstanten wie z.B π usw., und verschiedene logarithmische Skalen sind die einzigen Unterschiede zu unserem Gunterpaar.

12. Nähere Betrachtungen der Exponentialkurve

Die Kurve y = x², welche wir im Abschnitt 3 als Verbildlichung der Potenzreihe der Basis 2 gewannen, bildete schon zweimal den Ausgangspunkt von Betrachtungen, in deren Verfolg sich wertvolle Eindichten ergaben. Das eine Mal gewannen wir aus ihr die Bernoulli'sche Spirale und das andere Mal bildete sie die Grundlage für die Untersuchung des Verhältnisses verschiedener Logarithmensysteme zueinander. Sie führt in die Mathematik den Namen Exponentialkurve. Wir wollen von ihr zum dritten Male ausgehen, um eine wichtige Einsicht zu gewinneen.
Rufen wir uns zu diesem Zwecke in die Erinnerung zurück, wie sie entstand! Wir trugen in den äquidistanten (gleichweit voneinander entfernten) Punkten einer waagerechte Geraden, die die fortschreitenden Exponenten, -4, -3, -2, -1, 0, 1, 2, 3, 4, verbildlichten, die entsprechenden Potenzwerte, 2^-4, 2^-3, 2^-2, 2^-1, 2⁰, 2¹, 2², 2³, 2⁴, oder eben 1/16, 1/8, 1/4, 1/2, 1, 2, 4, 8, 16, als Senkrechte auf.

Potenzen		0		⋅⋅⋅⋅⋅		1/16		1/8		1/4		1/2		1		2		4		8		16		⋅⋅⋅⋅⋅		∞
Exponenten		- ∞		⋅⋅⋅⋅⋅		- 4		- 3		- 2		- 1		0		1		2		3		4		⋅⋅⋅⋅⋅		∞

Dann verbanden wir die Enden der Senkrechten geradlinig miteinander so, wie sie aufeinander folgten, und bekamen ein kurvenähnliches Gebilde, das aus lauter aneinandergereuhter Strecken bestand. Für die einzelnen Strecken, die sich immer steiler aufrichten, fanden wir ein bestimmtes Steigungsgesetz:

Die Steigung jeder Strecke ist ebensogroß wie die Längenzahl der Senkrechten ihres Anfangspunktes.

So ist in dem Exponenten 0 (Null) eine Senkrechte von der Länge 1, und die schräge Sehne, die im Endpunkt dieser Länge 1 nach rechts oben verläuft, hat gerade die Steigung 1 : 1 = 1. An der Stelle des Exponenten 1 befindet sich eine Senkrechte von der Länge 2, an deren oberem Endpunkte eine schräge Sehne von der Steigung 2 : 1 = 2 beginnt. An der Stelle des Exponenten 2 befindet sich eine Senkrechte von der Länge 4, in deren oberem Endpunkte eine schräge Sehne von der Steigung 4 : 1 = 1 beginnt. Usw. Dieses schöne Gesetz von der Übereinstimmung der Steigung einer Sehne mit der Länge der Senkrechten ihres Anfangspunktes muss ja wieder verlorengehen, wenn wir, wie geschehen, die Enden der Senkrechten krummlinig statt geradlinig verbinden; denn dann hat die Kurve zwischen zwei Senkrechten am Anfang eine geringere Steigung als ihre Sehne, am Ende eine größere Steigung, und irgendwo dazwischen ist ihre Steigung gleich derjenigen der Sehne, und dies alles darum, weil die Kurve zwischen den beiden Senkrechten nach unten durchhängt.
Insbesondere ist die schöne Steigung an der bedeutsamsten Stelle des Sehnenzuges, da, wo der Exponent den Wert 0 (Null) und die Sekrechte den Wert 1 hat, nämlich die Steigung 1 verlorengegangen. Die Kurve ist nun so beschaffen, dass ihre Steigung, die durch die Richtung ihrer jeweiligen Tangente repräsentiert wird, überall etwas kleiner als die Längenzahl der Senkrechten des betreffenden Kurvenpunktes ausfällt.
Gibt es keine Potenzreihe, deren Kurve an jeder Stelle ebenso stark ansteigt, wie es die Senkrechte des betreffenden Kurvenzuges angibt? Wenn es eine solche gäbe, wäre die Basis der Potenzreihe sicher nicht die Zahl 2. Da die nullte Potenz jeder Basis vom Werte 1 ist, müssen alle Exponentialkurven, auf welcher Basis sie auch aufgebaut sein mögen, über dem Exponenten 0 (Null) die Senkrechte 1 aufweisen. Auch die gesuchte, noch hypothetische Exponentialkurve müsste durch den Endpunkt dieser Senkrechten 1 über dem Exponenten 0 (Null) hindurchgehen. Dort müsste sie gemäß der von ihr vorausgesetzten Steigungseigenschaft dann genau die Steigung 1 besitzen. Während die Kurve y = x² durch jenen bedeutsamen Punkt so hindurchgeht, dass ihre Tangente dort schwächer geneigt ist als die Schräge der Steigung 1, müsste die gesuchte Exponentialkurve an jenem bedeutsamen Punkte die Schräge von der Steigung 1 oder, was dasselbe ist, von der Steigung 45° genau zur Tangente haben.
Um dieser Kurve auf die Spur zu kommen, wollen wir von der Basis 2 zu den beiden banchbarten Basen 1 und 3 übergehen und für jede derselben die Potenzreihe und ihre Verbildlichunh untersuchen:

Basis 1:



Potenzen		1- 4		1- 3		1- 2		1- 1		10		11		12		13		14		oder
		1		1		1		1		1		1		1		1		1
Exponenten		- 4		- 3		- 2		- 1		0		1		2		3		4


Die zugehörige Exponentialkurve ist, wie wir sofort erkennen, eine Parallele zur Exponentengerade im Abstand 1, d.h. diesmal ausnahmsweise keine krumme Linie. Sie hat als solche überall die Steigung 0 (Null), während ihre Senkrechten überall von der Länge 1 sind. Der Übergang von der Basis 2 zur Basis 1 hat uns also von der gesuchten Kurve, sofern sie überhaupt existiert, nur noch weiter weggeführt.

Basis 3:



Potenzen		3- 4		3- 3		3- 2		3- 1		30		31		32		33		34		oder
		1/81		1/27		1/9		1/3		1		3		9		27		81
Exponenten		- 4		- 3		- 2		- 1		0		1		2		3		4


Die zugehörige Exponentialkurve samt ihrem Sehnenzuge bietet folgendes Bild:






Die Steigungszahl der einzelnen Sehnen sind an dieselben darangeschrieben und lauten:



2/27 : 1

2/9 : 1

2/3 : 1

2 : 1

6 : 1


Von Sehne zu Sehne wächst die Steigung auf das Dreifache, wie es auch bei den Senkrechten der Fall ist. In einzelnen Zahlen umgeschrieben, lauten die aufeinanderfolgenden Sehnensteigungen:



2/27

2/9

2/3

2

6


Die Länge der Senkrechten am Anfang jeder Sehne beträgt:



1/27

1/9

1/3

1

3


Mithin beträgt hier die Sehnensteigung jedesmal das Doppelte der Längenzahl der Senkrechten am Anfabgspunkte der Sehne.
Beim Übergang vom Sehnenzuge zur Kurve geht diese Gesetzmäßigkeit wieder verloren. Die Kurve wird an allen ihrer Punkte etwas weniger steil als das Doppelte der Längenzahl der betreffenden Senkrechten. 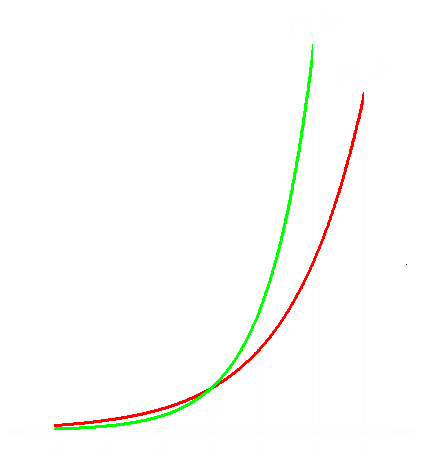Aber der bloße Anblick der Kurve lehrt bereits, dass die Kurvensteigung zwar unter das Doppelte der betreffenden Senkrechtenlänge heruntersinkt, aber nicht auch unter die Senkrechtenlänge selber; überall übertrifft die Steigung der Tangente die Längenanzahl der betreffenden Senkrechten.

Somit hat der Übergang von der Basis 2 zur Basis 3 die Steigungsverhältnisse der Kurve ins Gegenteil umschlagen lassen; bei der Basis 2 ist die Kurvensteigung allenthalben geringer als die Längenzahl der betreffenden Senkrechten, bei der Basis 3 allenthalben größer. Die von uns gesuchte Kurve, deren Charakteristikum in der Gleichheit von Kurvensteigung und Senkrechtenlänge bestehen soll, muss also zur Basis der Potenzen eine Zahl zwischen 2 und 3 besitzen. Sie ist auch räumlich zwischen den Exponentialkurven y = 2^x und y = 3^x gelegen. Sie zu finden, ist damit gleichbedeutend, ihre Basis zu ermitteln.

13. Stetige Kapitalisierung von Zinsen

Durch eine bestimmte, den Mathematikern seit zwei Jahrhunderten geläufige Denktechnik können wir uns die fragliche Kurve mit ihrer Basis zwischen 2 und 3 erobern. Ehe wir dies jedoch tun, wollen wir uns in der Art von Vorübungen mit jener Denktechnik etwas vertraut machen, indem wir sie in ein Lebensgebiet anwenden, mit dem wir umzuhejen gewohnt sind, auf dem Gebiet der Zinsberechnung von Kapitalien.
Es handele sich um ein sehr kleines Kapital, das wir Aleph oder ℵ nennen wollen. Das Aleph ist der erste Buchstabe des phönizischen und des hebräischen Alphabets und entspricht dem Alif der arabischen Schrift. Es steht für einen Konsonanten, den die Griechen, als sie das phönizische Alphabet an ihre Sprache anpassten, als Zeichen für den Vokal Alpha umdeuteten, woraus dann das lateinische A entstand. Der Name des Buchstabens leitet sich von der stilisierten Darstellung eines Stierkopfes (hebräisch alef: „Rind“) mit zwei Hörnern her. Im Verlauf der Schriftentwicklung wurde der Buchstabe gedreht und seine Form veränderte sich. Er hat den Zahlenwert 1.
Unser ℵ ist also zwar sehr klein, wird aber außerordentlich hoch verzinst. Der Zinfuß soll nicht weniger als 100% im Jahr betragen. Dann wird sich bei der Hinzufügung der Zinsen zum Kapital das letztere nach einem Jahr verdoppelt haben! Nach einem weiteren Jahre wird sich dieses auf 2 ℵ angewachsene Kapital wieder verdoppelt haben, also 4 ℵ betragen. Nach drei Jahren werden daraus 8 ℵ geworden sein usw. Wir sehen, die Reihe der Kapitalien am Anfang der einzelnen Jahre bildet unsere Potenzreihe auf der Basis 2:

1 ℵ

2 ℵ

4 ℵ

8 ℵ

16 ℵ

32 ℵ

⋅⋅⋅⋅⋅

Nun möge das Bankinstitut noch einen weiteren Vorteil gewähren, indem es die Zinsen nicht erst jährlich, sondern schon halbjährlich zum Kapital hinzuschlägt. Dann wird das Kapital nach einem vollen Jahr nicht bloß auf 2 ℵ, sondern auf 2,25 ℵ anwachsen. Denn nach einem halben Jahre sind 50 ℵ-Penny, also ℘, Zinsen aufgelaufen, die nun schon zum Kapital geschlagen werden, so dass sich für das zweite Halbjahr 1,50 ℵ verzinsen. Der halbjährige Zinsertrag dieser 1,50 ℵ beträgt 75 ℘, so dass am Ende des zweiten Jahres, wenn die Zinsen wieder zum Kapital hinzugefügt werden, 2,25 ℵ Kapital vorhanden sind. Man kann das Resultat auch folgendermaßen herausbekommen:

Aus 1 ℵ werden nach einem halben Jahr (1 + ½) ℵ, wofür man auch schreiben kann:



1 ⋅ (1 + ½)


Man erhält also das Kapital nach einem halben Jahre, indem man das Anfangskapital 1 mit dem Faktor (1 + ½), der auch Verzinsungsfaktor oder Diskontfaktor heißt, multipliziert. Mithin wird am Ende des zweiten halben Jahres aus dem Anfangskapital (1 + ½) ℵ das Endkapital (1 + ½)² ℵ geworden sein. Diese Potenz (1 + ½)² besitzt den Zahlenwert 3/2 ⋅ 3/2 = 9/4 = 2,25.

Auf dem eingeschlagenen Wege weiterschreitend, wollen wir nun annehmen, dass die halbjährliche Kapitalisierung der Zinsen zu einer vierteljährlichen, monatlichen, ja täglichen gesteigert werde.

Vierteljährlicher Zinseszins
Am Ende des ersten Vierteljahres ist unser Aleph auf (1 + 1/4) ℵ angewachsen. Da



1 + 1/4

=

1 ⋅ (1 + 1/4)


ist, beträgt jetzt der Verzinsungsfaktor (1 + 1/4). Mithin beläuft sich das Kapital am Ende des ersten Jahres auf



(1 + 1/4)4

=

(5/4)4

=

625/256

=

2,44 ℵ

Monatlicher Zinseszins
Der Zinsfaktor beträgt hier entsprechend (1 + 1/12). Daher erreicht das Kapital am Ende des ersten Jahres die Höhe



(1 + 1/12)12

=

(13/12)12

=

1,08333⋅⋅⋅12 ℵ


Wir berechnen diese hohe Potenz am besten logarithmisch:



log Kapital

=

log (1,0833312)

=

12 ⋅ log 1,08333


Wir können nicht erwarten, ein genaues Ergebnis herauszubekommen, da die Logarithmen unserer Referenztabelle ja Annäherungswerte sind. Die Ungenauigkeit wird umso größer werden, je wenigerstellig die verwendete Mantisse ist. Gilt dies bereits bei jeder logarithmischen Berechnung, so hier erst recht, da durch die Multiplikation mit 12 der Fehler ebenfalls verzwölffacht wird. Daher verwendet man bei Verzinsungsfaktoren höherstellige Logarithmen. Eine Tabelle, die eigens für Verzinsungsfaktoren entworfen wurde, listet siebenstellige Mantissen auf. Ihr kann man entnehmen:



log 1,08333⋅⋅⋅

=

0,034 7621 + 0


Durch Verzwölffachung erhalten wir:



log Kapital

=

0,417 1452 + 0


Die neue Mantisse reduzieren wir nun wieder auf vier Stellen:



log Kapital

=

0,4171 + 0


und erhalten:



Kapital

=

2,61 ℵ


Das Kapital von 1 ℵ ist also bei monatlicher Kapitalisierung der Zinsen auf 2,61 ℵ angewachsen.

Täglicher Zinseszins
Der Verzinsungsfaktor hat die Größe (1 + 1/365). Das Kapital erreicht daher nach einem Jahre den Betrag von



(1 + 1/365)365

=

(366/365)365

=

1,00274365 ℵ


Wieder berechnen wir die Potenz mit Hilfe der verfeinerten Mantissentabelle:



log 1,00274

=

0,001 1883 + 0


Die Multiplikation mit 365 ergibt:



log Kapital

=

0,433 7295 + 0

=

0,4337 + 0




Kapital

=

2,71 ℵ


Täglicher Zinseszins würde also bei einem Zinsfuß von 100% unseren einen Alephen auf 2,71 ℵ anwachsen lassen.

Kann dieser Betrag noch beliebig gesteigert werden, indem man die Kapitalisierung der Zinsen noch engmaschiger gestaltet? Wohin kommen wir bei stündlichem, minutlichem, ja sekundlichem Zinseszins? Wir gelangen jedesmal zu Ausdrücken von der Form

(1 + 1/n)n

worin n immer größer wird. Das Ende des Prozesses würde es bedeuten, wenn die Zinsen jeden Augenblick zum Kapitel hinzugefügt würden. Dies würde nach sich ziehen, dass in unserem Ausdruck die Zahl n über alles Maß wächst oder, wie der Mathematiker sagt, unendlich groß wird. Der Ausdruck selber wird dann aber nicht ebenfalls unendlich groß, sondern strebt einem bestimmten endlichen Werte zu, den man auch Grenzwert oder Limes des Ausdruckes nennt. Er ist jedoch niemals etwa in Form einer Dezimalzahl genau angehbar, sondern nur approximativ (annäherungsweise). Je höher man n hinauftreibt, je mehr es also dem Unendlichen zugeht, desto besser gelingt einem die Annäherung an den Grenzwert des Ausdruckes. Den Grenzwert selber kann man aber nur durch eine Buchstabenzahl andeuten. Als diese ist nach dem Vorgange des großen Baseler Mathematikers Leonard Euler (1707 bis 1783), dem wir, wie Bernoulli, bereits bei der Geschichte der Cornu-Spirale begegnet sind, der Anfangsbuchstabe e des Wortes Exponent gewählt worden:

e

=

lim (1 + 1/n)n

n

→

∞

Der Wert von e beträgt auf 12 Dezimalen errechnet:

e

=

2,718281828459

Daraus schließen wir, dass unser Kapital selbst bei stetiger Hinzufügung der Zinsen binnen eines Jahres niemals den Betrag von 2,72 ℵ erreichen würde.

Wenn alle diese Prozesse sich nicht bloß über den Zeitraum eines einzigen Jahres, sondern über mehrere Jahre erstrecken, ergibt sich die Kapitelsumme am Ende des 2., 3., 4., ⋅⋅⋅⋅⋅ Jahres durch entsprechende Potenzierung der Kapitalsumme am Ende des 1. Jahres:

Kapital am Ende des		1. Jahres		2. Jahres		3. Jahres		4. Jahres
Jährlicher Zinseszins		(1 + 1)1		(1 + 1)2		(1 + 1)3		(1 + 1)4
Halbjährlicher Zinseszins		(1 + 1/2)2		(1 + 1/2)4		(1 + 1/2)6		(1 + 1/2)8
Vierteljährlicher Zinseszins		(1 + 1/4)4		(1 + 1/4)8		(1 + 1/4)12		(1 + 1/4)16
Monatlicher Zinseszins		(1 + 1/12)12		(1 + 1/12)24		(1 + 1/12)36		(1 + 1/12)48
⋅⋅⋅⋅⋅		⋅⋅⋅⋅⋅		⋅⋅⋅⋅⋅		⋅⋅⋅⋅⋅		⋅⋅⋅⋅⋅
Augenblicklicher Zinseszins		e1		e2		e3		e4

Aus der ursprünglichen Basis (1 + 1/1)¹ = 2 wird also nacheinander die Basis

(1 + 1/2)2		=		9/4		=		2,25
(1 + 1/4)4		=		625/256		=		2,44 ⋅⋅⋅⋅
(1 + 1/12)12		=		(13/12)12		=		2,61 ⋅⋅⋅⋅
⋅⋅⋅⋅⋅
				e		=		2,718281828459

Wir wollen die entstandenen Verhältnisse nun auch noch graphisch verbildlichen:
Das Bild der Potenzreihe auf der Basis 2 kennen wir ja bereits; es stellt zugleich in Gestalt der einzelnen Senkrechten, die zu den Exponenten 0, 1, 2, 3, 4, ⋅⋅⋅⋅⋅ gehören, die Größe der Kapitalien am Anfang des ersten Jahres und am Ende des 1., 2., 3., 4., ⋅⋅⋅⋅⋅ Jahres dar. Die Exponenten haben nun eine Jahresbedeutung erhalten.
Das Bild der Potenzreihe auf der Basis (1 + ½)² = 2,25 unterscheidet sich vom vorigen durch Halbierung der Abstände zwischen den einzelnen Jahreszahlen.
Die Senkrechte am Anfang des ersten Jahres oder, was dasselbe ist, am Ende des nullten Jahres ist wieder 1. Die nächste Senkrechte erscheint schon beim Exponenten ½ und besitzt die Länge 2/3; zwischen ihr und der vorherigen Senkrechten beträgt die Steigung 45° oder 1. Die 3. Senkrechte steht über dem Exponenten 1 und besitzt die Länge (3/2)² = 2,25. An der gleichen Stelle befindet sich die Senkrechte der ursprünglichen Potenzreihe mit der Länge 2. Daher beträgt die Steigung zwischen den Sekrechten der Exponenten ½ und 1 mehr als 45°. Wie groß ist die genaue Steigung? Auf der waagerechten Länge ½ geht es um den Unterschied der beiden aufeinanderfolgenden Senkrechten, d.h. um 2,25 - 1,5 = 0,75 = ¾ hinauf. Die Steigung ist das Verhältnis der vertikalen Erhöhung zum horizontalen Fortschritt ¾ : ½ = 3/2, d.h. ebenso groß wie die Längenzahl der Senkrechten am Anfang der Schräge. So bleibt es auch, wenn wir die nächsten halben Jahre betrachten. Wie beim alten Sehnenzuge die einzelnen Senkrechten stets durch ihre Längenzahl auch die Steigung der in ihrem Endpunkte aufsteigenden Sehnen angaben, ist auch beim neuen Sehnenzuge, der doppelt so viel Senkrechte und damit doppelt so viel Sehnen enthält, die Längenzahl jeder Senkrechten zugleich auch die Maßzahl der Steigung der in ihrem Endpunkte aufsteigenden Sehne. Die Ineinanderzeichnung der beiden Sehnenzüge veranschaulicht diese Verhältnisse.
Schalten wir auf der Waagerechten nun sogar Viertel ein, so kommen wir zur Verbildlichunh des vierteljährlichen Zinseszinses. Es enstehen jetzt viermal so viel Senkrechten wie am Anfang und damit auch viermal so viel Sehnen. Der Sehnenzug steigt jetzt noch schneller hinauf. Wieder ist, wie man zeigen könnte, hier die Längenzahl jeder Senkrechten zugleich auch die Maßzahl der Steigung der im Endpunkte der Senkrechten beginnenden Sehne. Die Steigung der ersten der vielen kurzen Sehnen bleibt jedoch auch hier 45° oder 1.
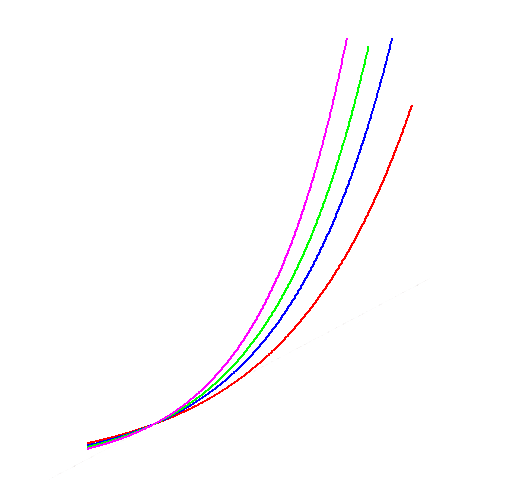Wir übergehen den nächsten Schritt, der eine Zwölftelung der einzelnen Jahre vorsieht, und begeben uns mit einem Sprung in das Ziel des Prozesses, die stetige Kapitalisierung der Zinsen, hinein. Die Jahresgerade ist nun in unendlich kleine Stücke aufgeteilt, und die Senkrechten sind unendlich viele geworden, die unendlich dicht nebeneinanderliegen. Zwischen den Endpunkten der unendlich vielen Senkrechten liegen unendlich viele, unendlich kurze Sehnen, deren Zug jetzt eine in den kleinsten Teilen krumme Linie konfiguriert. Die Basis des Ganzen ist die Zahl e geworden, und die "Gleichung" der Kurve lautet:

y

=

ex

In der Graphik zur rechten ist diese Kurve zu den drei Sehnenzügen hinzugezeichnet. Die Tangente an jeder Stelle der Kurve besitzt eine Steigung, deren Maßzahl mit der Maßzahl der Senkrechten des Berührungspunktes der Tangente übereinstimmt. Die Steigung der Kurve an ihrem Beginn, also für x = 0, ist gleich der Maßzahl der dort befindlichen Senkrechten, also gleich 1 oder 45°. Damit ist die Aufgabe, die wir uns im vorigen Abschnitt stellten, gelöst. Natürlich kann man nun diese Kurve über ihren Anfangspunkt auch nach der linken Seite fortsetzen, wenn auch dieser ausgezeichnete Teil keine unmittelbare Beziehung mehr zu dem hier erörterten Kapitalisierungsproblem hat. Der Gesamtkurve entspricht dann für ganzzahlige Exponenten das Reihenpaar:

Potenzen

0

⋅⋅⋅⋅⋅

1/e4

1/e3

1/e2

1/e

1

e

e2

e3

e4

⋅⋅⋅⋅⋅

∞

Exponenten

- ∞

⋅⋅⋅⋅⋅

- 4

- 3

- 2

- 1

0

1

2

3

4

⋅⋅⋅⋅⋅

∞

Aus 1 ℵ werden also im Laufe eines Jahres e = 2,71828⋅⋅⋅⋅ ℵ , wenn bei einem Zinsfuß von 100% die Zinsen augenblicklich kapitalisiert werden. Bei welchem Jahrezinsfuß wären aus 1 ℵ nach einem Jahr ebenfalls e ℵ geworden, wenn die Zinsen, wie üblich, erst am Ende des Jahres hinzugefügt worden wären? Natürlich hätte dann der Jahreszinsfuß noch weit mehr als 100% betragen müssen, nämlich, wie ersichtlich, 171,828⋅⋅⋅%, eine Zahl, die aus e entsteht, wenn man e - 1 = 1,71828⋅⋅⋅ bildet und dann verhundertfacht. 100% mit augenblicklicher Kapitalisierung bewirken also dasselbe wie 171,828⋅⋅⋅% mit jährlicher Kapitalisierung. Auf Grund eines Gegeneinanderhaltens der beiden Zahlen könnte man meinen, dass dann 50% mit augenblicklicher Kapitalisierung dasselbe wie 171,828⋅⋅⋅/2 = 85,914⋅⋅⋅% mit jährlicher Kapitalisierung bewirken würden. Das ist aber nicht der Fall, da zwischen den beiden zusammengehörigen Prozentsätzen, die wir kurz als gewöhnlichen und ungewöhnlichen Prozentsatz kennzeichnen wollen, eine verwickeltere Beziehung als diejenige der bloßen Proportionalität besteht. Wir wollen den ungewöhnlichen Prozentsatz, also den mit der augenblicklichen Kapitalisierung, durch die Buchstabenzahl x bezeichnen und den ihm in der Wirkung gleichbedeutenden gewöhnlichen Prozenzsatz durch die Buchstabenzahl y. Wie hier nicht weiter begründet werden soll, besteht dann zwischen x und y die Gleichung:

y

=

ex - 1

Wir wollen die Richtigkeit der Gleichung wenigstens für zwei uns bereits bekannte Fälle bestätigen:

1. Fall: Unverzinslichkeit.
In diesem Falle macht es keinen Unterschied, ob die nicht vorhandenen Zinsen augenblicklich oder erst am Ende des Jahres zum Kapital hinzugefügt werden; es ist ja x = y = 0. Dasselbe sagt auch unsere Gleichung, aus der durch Einsetzen von x = 0 und y = 0 wird:



		0		=		e0 - 1
oder		0		=		1 - 1

2. Fall: x = 100% = 1; y = 171,828⋅⋅⋅% = 1,71828⋅⋅⋅
Auch dieses Wertepaar "erfüllt" die gleichung; durch Einsetzen von x = 1 und y = 1,71828⋅⋅⋅ erhalten wir nämlich:



		1,71828⋅⋅⋅		=		e1 - 1
oder		1,71828⋅⋅⋅		=		e - 1
oder		1,71828⋅⋅⋅		=		2,71828⋅⋅⋅ - 1


Natürlich ist die Richtigkeit der Gleichung damit nicht förmlich bewiesen; dies müsste auf anderer Weise geschehen.
Da wir die Kurve mit der Gleichung y = e^x bereits kennen, ist es ein Leichtes, auch die neue Gleichung y = e^x - 1 zu verbildlichen. Wir brauchen in der vorigen Graphik unsere waagerechte Exponentengerade nur um die Länge 1 hinaufzudrücken, d.h. in die Lage AB zu bringen und haben dann das Bild der Gleichung y = e^x - 1 vor uns in dem Teil der Graphik, welcher durch die waagerechte Strecke AB, die senkrechte Strecke BC und den Kurvenbogen AC begrenzt ist. Wäre zwischen x und y kein Unterschied, d.h. y = x, so wäre das Bild nicht der Kurvenbogen AC, sondern die unter 45° aufsteigende Gerade AD. Die Kurve AC hat diese Gerade zur Tangante im Punkte A. An der Stelle A ist also noch kein Unterschied zwischen x und y; beide sind Null, und wir haben dort den schon besprochenen Grenzfall der Unverzinslichkeit vor uns. Kurz hinter A ist y, der gewöhnliche Zinsfuß, nur wenig größer als x, der ungewöhnliche Zinsfuß, nämlich genau so viel, wie die Kurve die schräge Gerade überragt. So könnte man zeigen, dass zu y = 3% gewöhnlichem Zinsfuße x = 2,96% ungewöhnlicher Zinsfuß gehören; dort überragt die Kurve die schräge Gerade um



3% - 2,96%

=

0,04%

=

0,0004


Man kann also sagen, dass bei unseren üblichen niedrigen Verzinsungssätzen, die ja um 3% herum liegen, die Hinzufügung der Zinsen am Ende eines Jahres fast gleichbedeutend mit einer stetigen Hinzufügung derselben ist. Erst wenn die Zinssätze erheblich höher werden, treten x und y merklich auseinander, um bei x = AB = 100% zu y = BC = 171,828⋅⋅⋅% zu führen.

Ist die Frage der augenblicklichen Hinzufügung von Zinsen nur eine rein theoretische, oder gibt es irgendwo Vorgänge, wo so etwas stattfindet? Durchaus! Zum Beispiel ist das pflanzliche Wachstum dem Anwachsen eines Kapitals auf Grund stetiger Zinszufügung zu vergleichen. Denken wir an den Holzbestand eines Waldes! Dort ist ja das Wachstum proportional der jeweils vorhandenen Menge lebendiger Zellsubstanz, im Sommer allerdings stärker als im Winter. Überall, wo sich lebendige Substanz vermehrt, wird die hinzukommende Substanz im Augenblicke ihres Entstehens ein Bestandteil der Gesamtsubstanz und ist nun an der Hervorbringung weiterer Substanz mitbeteiligt.

14. Die Exponentialkurve y = e^x und die Spirale r = e^b

Unter den vielen möglichen Exponentialkurven nimmt die zuletzt besprochene mit der Gleichung y = e^x eine Sonderstellung ein. Nur bei ihr ist ja die Steigung jeweils gleich der Maßzahl der betreffenden Senkrechten, und sie allein hat demgemäß an bedeutsamsten Punkte der Kurve, über dem Exponenten 0 (Null), die Steigung 1 oder 45°. Was verstehen wir denn unter Steigung? Das Verhältnis der vertikalen Erhebung zum entsprechenden horizontalen Fortschreiten! Wandern wir den Abhang eines Berges hinauf, so kommen wir gleichzeitig vorwärts und aufwärts, und das Aufwärts, an dem Vorwärts gemessen, liefert die Steigung des Abhanges. Wählen wir als einen solchen Abhang irgendeine Tangente unserer Kurve y = e^x, und beginnen wir unsere Wanderung da, wo diese Tangente die Exponentengerade schneidet, so können wir die Tangente bis hinauf zum Berührungspunkte - welches Stück man auch Tangente im engeren Sinne nennt - erklimmen. Dann werden wir als Höhe gerade die Senkrechte y des Berührungspunktes erklommen haben. Um welches Stück sind wir dabei waagerecht vorwärts gekommen? Da das Verhältnis des Vertikalen zu seinem Horizontalen hier und nur hier mit der Zahl des Vertikalen übereinstimmt, besteht die Gleichung:

vertikaler Aufstieg horizontalen Fortschritt

=

vertikalem Aufstieg

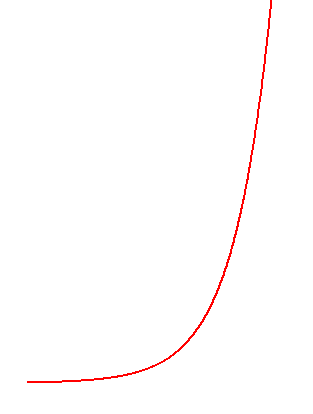Hier ist also ein Bruch gleich seinem Zähler. Das ist nur möglich, wenn sein Nenner von der Zahl 1 gebildet wird. Der dem vertikalen Aufstieg y entsprechende horizontale Fortschritt muss also beim Erklimmen der Tangente die Länge 1 betragen haben. Somit ist das unter jeder Tangente liegende Stück der Exponentengeraden, welches auch Subtangente genannt wird, von der gleichen Länge 1. Unsere Exponentialkurve ist die einzige Kurve mit lauter gleichen Subtangenten. Verbinden wir daher einen Punkt der waagerechten Exponentengerade, welcher einer der Exponenten

⋅⋅⋅⋅⋅

-3

-2

-1

0

1

2

3

⋅⋅⋅⋅⋅

entspricht, mit dem Endpunkt der Senkrechten des folgenden Exponentenpunktes, so ist diese Verbindungslinie immer eine Tangente der Exponentialkurve. Dieser Tatbestand ist in der Graphik zur Linken verwertet worden. Dort nehmen wir insgesamt sechs rechtwinklige Dreiecke wahr, deren Kathete stets die Länge 1 besitzt. Die andere Kathete durchläuft von links nach rechts die Zahlen e^-2, e^-1, 1, e, e², e³, und die Hypotenuse der Dreiecke sind Tangenten der Exponentialkurve. Das mittlere der sechs Dreiecke ist gleichschenklig-rechtwinklig und gruppiert die linken und rechten Dreiecke zu zusammengehörigen Paaren. So bilden die dem mittleren Dreick unmittelbar benachbarten Dreiecke insofern ein Paar, als sie beide dieselbe Form haben, also ähnlich sind; das rechte Dreieck ist nur die e-fache Vergrößerung des linken und dabei um 90° gedreht. Ebenso ist es mit dem nächsten Paar Dreiecke; die Vergrößerungszahl vom kleinen zum großen Dreieck ist dort e². Vom kleinsten Dreieck ganz links zum größten Dreieck ganz rechts gelangt man durch die Vergrößerungszahl e³.
Wie wir in Abschnitt 4 aus der Kurve mit der Gleichung y = 2^x eine Bernoulli'sche Spirale von der Gleichung r = 2^b gewannen, kann man aus der bedeutsamsten Exponentialkurve, deren Gleichung y = e^x lautet, die bedeutsamste Bernoulli'sche Spirale mit der Gleichung r = e^b hervorgehen lassen. Zu ihr gehört also das Reihenpaar

Radien r		⋅⋅⋅⋅⋅		e-3		e-2		e-1		1		e		e2		e3		⋅⋅⋅⋅⋅
Bögen b		⋅⋅⋅⋅⋅		- 3		- 2		- 1		0		1		2		3		⋅⋅⋅⋅⋅

Unter dem Bogen b = 1 ist dabei ein Bogen zu verstehen, der durch einen Winkel von 360°/2π = 57° 17' 44,8'' im Kreise vom Radius 1 erzeugt wird. Der Bogen 2 entspricht dem doppelten Winkel in diesem Kreise, usw. Dem Winkel 360° entspricht der Bogen b = 2π = 2 ⋅ 3,14159⋅⋅⋅ = 6,28318⋅⋅⋅ Die Spirale ist in folgender Abbildung klassisch zu konstruieren versucht worden. Man kann wegen des mächtigen Schwunges von ihr nicht einmal eine einzige Windung um den Pol herum zeichnen. Eine solche volle Windung würde z.B. von der Stelle b = 0 bis zur Stelle b = 2π reichen. Für b = 0 ergibt sich r = e⁰ = 1, und für b = 2π erhalten wir r = e^2π = 535,4⋅⋅⋅; im Laufe einer vollen Windung steigt also die anfängliche Entfernung vom Pole P rund auf den 535fachen Betrag. Selbst wenn wir also die anfängliche Entfernung nur 1 mm groß wählen würden, wäre die Entfernung nach einer vollen Umwindung des Poles schon auf 353 mm = 53,5 cm angewachsen. In unserer Figur ist etwas mehr als eine halbe Windung hingezeichnet.
Welches ist die gerade diese Spirale auszeichnende Eigenschaft? Man könnte zeigen, dass an allen Punkten B dieser Spirale der Radius PB mit der Tangente in B einen Winkel von 45° oder einen halben Rechten bildet. Auf Grund dieser Eigenschaft kann man sich eine mechanische Erzeugung dieser Spirale vorstellen. Ein in einem Punkte P, dem Pole der zu erzeugenden Spirale, befestigter unendlich langer Zeiger dreht sich um P herum, während ein Punkt B sich von P den Zeiger entlang entfernt. Die beiden Bewegungen sind dann in jedem Augenblicke zueinander sekrecht. Wenn sie überdies in jedem Augenblicke auch von gleicher Stärke sind, muss ja der Punkt B in der Dreh-Ebene des Zeigers eine Spirale beschreiben, deren Tangenten gegen die jeweiligen Zeigerstellungen unter einem halben Rechten oder 45° gewinkelt sind. Das ist aber die Spirale von der Gleichung r = e^b. Damit die beiden Bewegungsimpulse, wie notwendig, in jedem Moment der Bewegung von gleicher Stärke sind, dürfen interessanterweise die Gleitbewegung von B auf dem Zeiger und die Drehbewegung des Zeigers nicht beide zugleich gleichmäßig schnell vor sich gehen. Denn nehmen wir etwa an, der Zeiger drehe sich mit gleichmäßiger Geschwindigkeit um P herum! Er bestreicht ja dann in seiner gleichmäßigen Drehung die Bögen b = 0, 1, 2, 3,⋅⋅⋅⋅ Damit B in der Zeigerebene die Spirale r = e^b beschreibt, muss B nacheinander die entsprechenden Entfernungen r = 1, e, e², e³,⋅⋅⋅⋅ vom Pol P annehmen, d.h. aber, sich mit wachsender Schnelligkeit nach außen bewegen. Würde dagegen die Gleitbewegung von B auf dem Zeiger eine gleichförmige Geschwindigkeit aufweisen, so müsste sich die Drehbewegung des Zeigers dauernd verlangsamen. Zu einer gleichmäßigen Drehung gehört also eine beschleunigte Gleitbewegung, zu einer gleichförmigen Gleitbewegung eine verzögerte Drehung. Sonst wären eben beide Bewegungen in jedem Momente der Bewegung nicht von gleicher Stärke, und der erforderliche Winkel von 45° würde verfehlt. Wären beide Bewegungen zugleich gleichförmig, so entstünde eine gewöhnliche oder Archimedische Spirale, bei der die Entfernung r vom Pol stets der stattgehabten Drehung proportional ist.
In der Unveränderlichkeit des Winkels zwischen einer Tangente der Spirale und dem Radius ihres Berührungspunktes erkennen wir die im Abschnitt 11 behandelte Loxodrome wieder. Dort stellten wir uns ein Schiff vor, das mit gleichbleibendem Kurse auf den Nordpol zusteuert. Dann muss es eine sphärische Loxodrome beschreiben, die sich in der Nähe des Nordpols von einer Bernoulli'schen Spirale kaum unterscheidet. Nur in dem Falle, dass der Kurs des Schiffes einer der vier Haupthimmelsrichtungen folgt, käme keine eigentliche Spiralbewegung zustande, sondern bei Nordsüdkurs eine Fahrt längs eines Meridiankreises, bei Ostwestkurs eine Fahrt längs des Breitenkreises. Der Nordsüdkurs entspricht dabei der vorhin bei der mechanischen Erzeugung der Spirale vorausgesetzten geradlinigen Gleitbewegung, der Ostwestkurs der Zeigerdrehung. Im Falle, dass das Schiff immer genau Nordwestkurs oder Nordostkurs einhält, kommt um den Pol herum praktisch die Spirale von der Gleichung r = e^b zustande. Das Schiff möge sich auf seiner Spiralfahrt völlig gleichmäßig bewegen, d.h. seine Geschwindigkeit möge sich weder vergrößern oder verringern. Dann muss die Umkreisung des Nordpoles immer schneller vor sich gehen. Die Windungen werden ja bald so eng, dass wir dem Schiffskörper fast keine Ausdehnung mehr beilegen dürfen; er schrumpfte mehr und mehr in einen sich bewegenden Punkt zusammen. Dieser Punkt, der sich also auf der Spirale gleichmäßig schnell bewegt, wird dann um den Pol herum eine immer rasender werdende Drehbewegung beschreben müssen. Noch vor Erreichung des Poles müsste er wegen der gewaltigen Zentrifugalkräfte zerplatzen! Wenn er dann den Pol endlich doch erreicht hätte, wäre seine Tourenzahl unendlich groß geworden. Kein Wunder also, dass sich der Kapitän unseres kleinen Schiffes dazu entschlossen hat, wieder umzukehren und einen Südwestkurs einzuschlagen, wie das Bild links nun zeigt.
Aber, so fragen wir, Kann der Punkt den Pol überhaupt erreichen? Ist nicht sein Weg bis dahin wegen der Unzahl der allerdings unfassbar eng werdenden Windungen um den Pol herum unendlich lang, so dass er, zeitlich gesehen, niemals am Ziele ankommen kann? Nein, so ist es nicht! Der Weg von einer beliebigen Stelle A der Fahrt bis zum Nordpol P ist nur von endlicher Länge. Man kann sogar mit Hilfe höherer Mathematik genau berechen, wie lang er ist. Nennen wir, wie üblich, die Entfernung einer solchen beliebigen Stelle A zum Nordpol r, wobei wir den Unterschied zwischen sphärischer Loxodrome und Bernoulli'scher Spiral endgültig fallen lassen, so ist die Fahrtlänge von A bis P, d.h. der Spiralenbogen, durch folgende sehr einfache Konstruktion zu ermitteln: man errichte über r = AP das Quadrat und zieht in diesem eine Diagonale, am besten die, welche mit der Spiralentangente in A zusammenfallen muss. Die Länge AP' dieser Diagonale gibt dann die Länge des Spiralenbogens AP an. Diese Konstruktion ist allerdings nur für die Spirale r = e^b, d.h. also, um in unserem Bilde zu bleiben, nur für genauen Nordost- oder Nordwestkurs, gültig. Die Figur, auf die wir uns hier bezogen, zeigt noch, in welchen Abständen die einzelnen Fahrtstationen B, C, D, E, F, G, H,⋅⋅⋅⋅, die lauter gleichen Winkeln am Pol entsprechen, sich auf die Fahrtlänge AP' verteilen. Um dies zu finden, braucht man nur einen Radius, z.B. PB, auf der Vertikalen PP' von P' aus bis B'' abzutragen und dann von B'' waagerecht auf die Diagonale AP' nach B' herüberzugehen.

15. Die natürlichen Logarithmen

Wir kehren nun zur Betrachtung der Exponentialkurve mit der Gleichung y = e^x zurück, wie wir sie im vorigen Abscnitt vor uns hatten und drehen diese Zeichnung um 90° gegen den Uhrzeigersinn, so wirde aus den bisherigen Waagerechten wird nun ein Senkrechtes und umgekehrt. 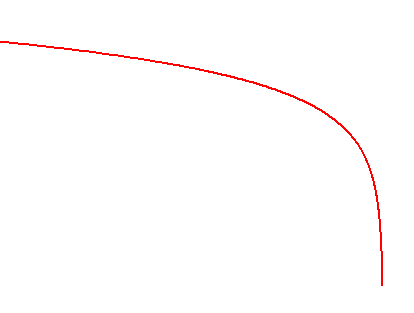Während für die normale Betrachtungsart die Kurve ganz links fast waagerecht ist und, nach rechts durchlaufend, immer steiler wird, an ihrem bedeutsamen Punkte die Steigung 45° durchschreitet, steigt für die neue Betracchtungsart die Kurve aus unendlicher Tiefe nach links hin auf, zuerst sehr steil, dann sich bis zu ihrem bedeutsamen Punkt allmählich auf 45° abflachend, um dahinter noch flacher und fast waagerecht zu werden. Aus dem früheren Verhältnis des Vertikalen zum entsprechenden Horizontalen wird jetzt das umgekehrte Verhältnis. Da, wo z.B. für die frühere Anschauung die Steigung 5 : 3 bestand, herrscht jetzt die Steigung 3 : 5. Nehmen wir nun noch die Steigungseigenschaft gerade dieser Kurve hinzu, so sind hinter dem bedeutsamen Punkte statt der zunehmenden Steigungen e, e², e³,⋅⋅⋅⋅ die abnehmenden Steigungen e^-1, e^-2, e^-3,⋅⋅⋅⋅ vorhanden, und von einer dieser Steigungen zur nächsten gewinnt man immer die Maßeinheit an Höhe. Die so angesehene Exponentialkurve trägt den Namen "Logistika". Ihre "Gleichung" ist natürlich ebenfalls y = e^x. Will man jedoch den neuen Aspekt, den die Kurve bietet, auch in der Gleichung zum Ausdruck bringen, so muss man die alte Gleichung umschreiben. In dieser stand das frühere Vertikale, also y, fertig ausgerechnet vor uns:

y

=

ex

Das neue Vertikale liegt in der Buchstabenzahl x beschlossen, und diese muss jetzt fertig ausgerechnet vor uns stehen, das heißt aber

x

=

elog y

Damit stoßen wir auf dasjenige Logarithmussystem, welches zu Basis die Zahl e hat. Es wird unter den vielen möglichen Logarithmensystemen ebenfalls eine Sonderstellung einnehmen. Diese kommt in dem Namen zum Ausdruck, welchen man gerade diesem Logarithmensystem gegeben hat; man hat es das natürliche Logarithmensystem geheißen. Das dekadische Logarithmensystem hat man wohl auch künstliches Logarithmensystem genannt - das mayaische Logarithmensystem wahrscheinlich nur das bekloppte Logarithmensystem. So wichtig das dekadische Logarithmensystem für das praktische Rechnen ist, so wichtig ist das natürliche für mathematische Betrachtungen höherer Art. Aus unserer Referenztabelle kann man die natürlichen Logarithmen auf Grund der Proportion errechnen:

nat. log z   dek. log z		=		nat. log e   dek. log e
		=		1  0,4343
nat. log z		=		dek. log z    0,4343

Mit diesen natürlichen Logarithmen haben wir schon zu tun gehabt, ohne uns dessen bewusst zu sein. Um das zu verstehen, müssen wir durch eine Art Rückschau etwas weiter ausholen:

Die Exponentialkurve mit der Gleichung y = e^x enträtselte uns ja durch die Problemstellung, eine krumme Linie zu finden, deren Steigung an jeder Stelle ebenso groß sein möchte wie die Zahl der Länge der Senkrechten, die auf der waagerechten Achse errichtet wird. Auf dieses Problem gerieten wir von einer anderen Exponentialkurve her, der Kurve mit der Gleichung y = 2^x. Diese war ja so zustande gekommen, dass wir das Reihenpaar

Potenzen		0		⋅⋅⋅⋅⋅		1/16		1/8		1/4		1/2		1		2		4		8		16		⋅⋅⋅⋅⋅		∞
Exponenten		- ∞		⋅⋅⋅⋅⋅		- 4		- 3		- 2		- 1		0		1		2		3		4		⋅⋅⋅⋅⋅		∞

in der gewohnten Art verbildlichten und die Endpunkte der aufeinanderfolgenden Senkrechten zunächst durch schräge Strecken verbanden. Dabei zeigte sich, dass die Schräge oder Steigung jeder dieser Strecken, als Zahl gefasst, ebenso groß war wie die Zahl der Länge der Senkrechten am Beginn der Strecke. Sodann verbanden wir die Endpunkte aller Senkrechten nacheinander durch eine wohlgeschwungene krumme Linie, eben unsere Exponentialkurve mit der Gleichung y = 2^x. Die Aufeinanderfolge der schrägen Strecken wurde nun zu einem Sehnenzug dieser Kurve. Durch den Übergang von dem Sehnenzug zur Kurve ging aber das schöne Gesetz der Steigung verloren; denn die Kurve besaß an jeder ihrer Stellen eine Steigungszahl, die nicht mehr gleich der Längenzahl der betreffenden Senkrechte war, sondern kleiner, und das Problem erwuchs, eine Kurve zu finden, bei der das Steigungsgesetz des Sehnenzuges erhalten bleibt.Um diese damals noch hypothetische Kurve zu finden, fassten wir eine andere Exponentialkurve ins Auge, jene mit der Gleichung y = 3^x. Bei ihr nahmen wir durch bloßen Augenschein wahr, dass an jeder Stelle ihre Steigung etwas größer war, als die Zahl der zugehörigen Senkrechten ist. Zwischen den beiden Exponentialkurven mit den Gleichungungen y = 2^x und y = 3^x musste somit die gesuchte Exponentialkurve liegen; ihre Basis war entsprechend zwischen den Basen 2 und 3 gelegen. Durch das Problem der augenblicklichen Kapitalisierung der Zinsen bei einem Zinsfuß von 100% kamen wir der gesuchten Kurve auf die Spur; ihre Basis war die tatsächlich zwischen 2 und 3 gelegene Zahl

e		=		lim (1 + 1/n)n
				n → ∞
		=		2,71828⋅⋅⋅⋅

Wenn bei den Exponentialkurven mit den Gleichungen y = 2^x und y = 3^x das erwähnte Steigungsgesetz verlorengegangen ist, so bedeutet das nicht, dass nicht auch an ihnen ein Steigungsgesetz waltet. Dasselbe ist sogar verhältnismäßig einfach auszusprechen, wenn auch seine Begründung auf elementarem Wege zwar nicht unmöglich, aber doch ziemlich mühsam ist. Wir wollen uns darum hier dieser Begründung versagen und nur das Ergebnis zur Kenntnis nehmen. Es zeigt sich nämlich, dass bei der Kurve der Gleichung y = 2^x die Steigung an jeder Stelle der gleiche Bruchteil der Zahl der zugehörigen Senkrechten und bei jeder Kurve der Gleichung y = 3^x die Steigung an jeder Stelle das gleiche Vielfache der Zahl der zugehörigen Senkrechten ist. Um zu verstehen, wie dies gemeint ist, könnten wir uns ja eine Kurve denken, deren Steigung an jeder Stelle halb so groß ist wie die Zahl der Senkrechten; dann wäre doch an jeder Stelle die Steigung der gleiche Bruchteil der Zahl der zugehörigen Senkrechten. Oder wir dächten uns eine Kurve, deren Steigung an jeder Stelle das Doppelte der Zahl ihrer zugehörigen Senkrechten ist; dann wäre an ihr die Steigung an jeder Stelle das gleiche Vielfache der Zahl der zugehörigen Senkrechten. Die Unterscheidung zwischen gleichem Bruchteil und gleichem Vielfachen kann man fallen lassen, indem man beide Male von einem gleichen Vielfachen spricht. Dann wäre im ersten Verdeutlichungsbeispiel die Vervielfachungszahl ½, im zweiten Verdeutlichungsbeispiel die Vervielfachungszahl 2.So können wir das Steigungsgesetz unserer beiden Kurven y = 2^x und y = 3^x auch folgendermaßen ausdrücken: bei beiden ist die Steigung an jeder Stelle das gleiche Vielfache der Zahl der zugehörigen Senkrechten. Welches nun die in Frage kommende Vervielfachungszahl in jedem der beiden Fälle ist, ist überraschend. Bei der Basis 2 ist die Vervielfachungszahl der natürliche Logarithmus der Zahl 2, wogegen bei der Basis 3 die Vervielfachungszahl der natürliche Logarithmus der Zahl 3 ist.
Aus unserer Referenztabelle rechnen wir um:

nat. log 2

=

dek. log 2    0,4343

=

0,3010 0,4343

=

0,6931

≈

0,7

nat. log 3

=

dek. log 3    0,4343

=

0,4771 0,4343

=

1,0986

≈

1,1

Die Kurve y = 2^x hat demnach überall eine Steigung vom ungefähren Werte der 0,7fachen der Zahl der zugehörigen Senkrechten, wogegen die Steigung bei der Kurve y = 3^x überall vom ungefähren Werte des 1,1fachen der zugehörigen Senkrechten ist. So ist einer Exponentialkurve an allen ihrer Stellen der natürliche Logarithmus ihrer Basis sozusagen eingeschrieben.. Man braucht nur an irgendeiner Stelle der Kurve die Senkrechte und die Steigung zu messen und dann die Übergangszahl von der Senkrechten zur Steigung aufzusuchen, um den natürlichen Logarithmus der der Kurve zugrunde liegenden Basis vor sich zu haben. Dieser tritt sogar nicht bloß als Übergangszahl zwischen Senkrechter und Steigung, sondern direkt als Steigungszahl selber im bedeutsamen Punkte jeder Exponentialkurve auf, da, wo der Exponent vom Werte 0 (Null) und die Senkrechte stets vom Werte 1 ist. In diese Zusammenhänge ordnet es sich auch ein, dass die Steigung der Kurve y = e^x überall gleich der Zahl der zugehörigen Senkrechten ist. Wie groß müsste denn an ihr die Vervielfachungszahl beim Übergange von der Senkrechten zur Steigung sein? Offenbar gleich dem natürlichen Logarithmus der Zahl e! So kommt bei der Kurve y = e^x die Übereinstimmung zwischen der Steigungszahl und der Zahl der zugehörigen Senkrechten zustande.
Es nimmt uns nun auch nicht mehr Wunder, zu erfahren, dass auch andere Exponentialkurven als die auf der Basis e zum Problem der augenblicklichen Kapitalisierung von Zinsen einen Bezug haben. Die Kurve y = e^x gehörte bei diesem Problem zum Zinsfuße von 100%. Diese 100% bedeuten ja nichts anderes als 100 Hunderstel oder die Zahl 1, d.h. aber jener Zahl, welche zugleich die vorhin behandelte Vervielfachungszahl der Kurve y = e^x bedeutete:

Kurve

y = ex,

Vervielfachungszahl

=

nat. log e

=

1

=

100%

Liegt es da nicht nahe, für die anderen Exponentialkurven eine ebensolchen Zusammenhang zu vermuten? Also beispielsweise:

Kurve

y = 2x,

Vervielfachungszahl

=

nat. log 2

=

0,6931⋅⋅⋅⋅

=

69,31%

Kurve

y = 3x,

Vervielfachungszahl

=

nat. log 3

=

1,0986⋅⋅⋅⋅

=

109,86%

Wenn es dem so wäre, so würde dies heißen:

1. Ein Kapital, welches zu 69,31⋅⋅⋅⋅% auf Zinseszinsen stünde, müsste sich bei stetiger Verzinsung nach einem Jahr verdoppeln, nach 2 Jahren vervierfachen, nach 3 Jahren verachtfachen usw. Seine Wachstumskurve wäre die Kurve mit der Gleichung y = 2^x. Dann wären die 69,31⋅⋅⋅⋅% der ungewöhnliche Prozentsatz, dem naturgemäß 100% gewöhnlicher Prozentsatz entsprächen.
2. Ein Kapital, welches zu 109,86⋅⋅⋅⋅% auf Zinseszinsen stünde, müsste sich bei stetiger Verzinsung nach einem Jahr verdreifachen, nach 2 Jahren verneunfachen, nach 3 Jahren versiebenundzwanzigfachen usw. Seine Wachstumskurve wäre die Kurve mit der Gleichung y = 3^x. Dann wären die 109,86⋅⋅⋅⋅% der ungewöhnliche Prozentsatz, dem naturgemäß 200% gewöhnlicher Prozentsatz entsprächen.

So, wie es oben vermutet wurde, ist es auch wirklich. Jede Exponentialkurve ist die Wachstumskurve eines stetig verzinsten Kapitales. Der Zinfuß ergibt sich einfach dadurch, dass man von der Basis der Exponentialkurve den natürlichen Logarithmus bildet. Auch von dieser Seite her fällt also auf die natürlichen Logarithmen ein Licht.

16. Die Tonwahrnehmung - Das Weber-Fechner'sche Gesetz der Psychophysik

Nun, da wir die Logarithmen näher kennengelernt haben, können wir einen Moment innehalten und bei etwas ruhiger Klaviermusik unseren Tee genießen. Wir hören das sogenannte "Regentropfen-Prélude" von Frédéric Chopin; es ist das 15. von insgesamt 24 Préludes, welche er 1838/39 komponierte als er krankheitsbedingt auf der Mittelmeerinsel Mallorca weilte. Ein besonderes Merkmal, das dieses in Des-Dur gehaltene Stück besonders auszeichnet, ist die stete monotone Wiederholung eines bestimmten Tones, womit der Anschein gleichmäßig fallender Tropfen erweckt wird. Sehen wir im Notenblatt des Stückes nach, erkennen wir, dass es sich dabei um das "as" bzw. "gis" handelt. Das Bild zur rechten zeigt uns, dass es sich bei dem Ton as/gis um dieselbe Taste handelt - die Nebentaste zwischen den Tasten g und a. Auf einem gut gestimmten Klavier erzeugt diese Taste einen Ton mit der Frequenz 207,65 Hertz (Hz).

Was hat dies mit Logarithmen zu tun? Mehr als man glauben mag! Es geht um die Wahrnehmung von Tönen durch das menschliche Ohr. In der Mathematik vergleicht man Zahlen miteinander; dies kann entweder ein unterscheidender Vergleich (64 | 4 = 60) mit den Operationen Addition (+) und Subtraktion (-), ein messender Vergleich (64 ⋅⋅ 4 = 16) mit den Operationen Multiplikation (⋅) und Division (:) oder ein logarithmischer Vergleich (log 64 = 4) mit den Operationen Potenzieren (x^y) und Radizieren (^y√x) sein. Dieselbe Dreistufigkeit findet sich auch in der Wahrnehmung der Töne durch das menschliche Ohr, wenn dieses vor der Aufgabe steht, entweder einen einzigen Ton oder ein Tonpaar oder eine Tonvielfalt, zumindest eine Tondreiheit, aufzufassen.
Beginnen wir mit dem Erlebnis des einzelnen Tones. Dabei beschränken wir uns auf die eingestrichene chromatische Tonleiter wie sie im obigen Bild dargestellt ist:

Dieses Bild ist verweissensitiv!

Auf einem chromatisch richtig gestimmten Klavier - was bei dem hier gebrauchten leider nicht der Fall war! - hat jeder dieser Töne rein physikalisch gesehen folgende Frequenzen:

Ton				c'				d'				e'				f'				g'				a'				h'
Frequenz [Hz]				261,63				293,66				329,63				349,23				392,00				440,00				493,88

Dazu kommen noch die Halbtöne

Ton				cis'/des'				dis'/es'				fis'/ges'				gis'/as'				ais'/b'
Frequenz [Hz]				277,18				311,13				369,99				415,30				466,16

Besondere Bedeutung kommt dabei dem Ton a' zu; er wird zum Stimmen von Instrumenten verwendet. Dazu wurde früher eine Stimmgabel benutzt, die genau auf diese 440,00 Hz geeicht war. Ich erinnere mich noch, als ich als kleiner Bub ein altes Klavier geschenkt bekam. Der alte Klavierbauer, der es nach dem Transport stimmte, benutze wirklich nur diese eine Stimmgabel als Referenz zu jedem einzelnen Ton. Ich war zutiefst beeindruckt.
Der alte Klavierbauer hatte natürlich einige Tricks auf Lager, die mir damals völlig fremd waren. Einen dieser Tricks bezeichnet der Physiker und auch der Akustiker als Schwebung. Was das bedeutet, verstehen wir, wenn wir den Einzelton im Momente seiner Entzweiung ergreifen, d.h. wenn wir zwei im Grunde verschiedene Töne erklingen lassen, die sich in der Tonwahrnehmung jedoch als ein einziger Ton darstellen. Die meisten Menschen besitzen kein so geschultes Ohr wie unser alter Klavierbauer, daher greifen wir auf einen Sinusgenerator zurück und spielen zu unserem Grundton a' (440 Hz) einen zweiten hinzu, z.B. eine Sinusschwingung von 441 Hz:

440 Hz + 441 Hz

Wie das technische Oszilloskop - rechter Link - vernehmen auch wir bei ihrem gleichzeitigen Erklingen nur einen Ton, aber wir hören ihn vibrieren; einmal schwillt seine Stärke in der Sekunde an und ab. In dieser Erscheinung, die Schwebung, nimmt das Ohr den Unterschied der beiden Schwingungsmengen, der je eine Schwingung pro Sekunde beträgt, wahr. Dass es dieses kann, ist gar nicht einmal etwas Erstaunliches. Denn der akustische Luftvorgang selber ruft diese Unterschiedszahl durch die ja jedem Physiker bekannte Erscheinung der sogenannten Interferenz von Schwingungen hervor. Diese Fähigkeit des Ohres, die Anzahl der Schwebungen eines solchen Doppeltones in der Sekunde zu zählen, ist also rein äußerlich erklärbar und bedingt. Das Ohr müsste schlecht organisiert sein, wenn es die äußerlich vorhandenen Vibrationen dieses Doppeltones nicht wahrnehmen könnte.
Vergrößern wir die Unterschiedszahl etwa auf 2 Schwingungen pro Sekunde indem wir zu dem a' eine Sinusschwingung von 442 Hz einspielen, so raten wir schon, was passiert:

440 Hz + 442 Hz

Die Anzahl der Schwebungen pro Sekunde verdoppelt sich auf 2! Das Oszilloskop sowie wir können die beiden verschiedenen Töne jedoch nicht auflösen; sie klingen zusammen wie ein einziger Ton. Einen Graubereich betreten wir beim Zuspielen von 460 Hz. Zwar können wir diese Töne noch immer nicht auflösen, doch das Oszilloskop zeigt einen leicht breiteren und verwascheneren Streifen an:

440 Hz + 460 Hz

Vergrößern wir nun die Unterschiedszahl weiter auf 40 Schwingungen pro Sekunde, so können wir bei einem guten Gehör gerade zwei unterschiedliche Töne wahrnehmen, die sehr schnell miteinander vibrieren. Das Oszilloskop zeigt nun ganz deutlich zwei Spektralstreifen an:

440 Hz + 480 Hz

Man kann also sagen, dass die Auflösungsgrenze, ab der wir zwei Töne unterscheiden können, bei einer Unterschiedszahl von ungefähr 40 Schwingungen pro Sekunde liegt. Liegt die Unterschiedszahl unter diesen 40 Schwingungen pro Sekunde, nehmen wir Schwebungen wahr, liegt sie darüber, können wir ein "Zwischen den Tönen" wahrnehmen. Diese Auflösungsgrenze gilt auch für den höheren Frequenzbereich, wie das folgende Beispiel zeigt:

1000 Hz + 1030 Hz

Hierbei beginnen wir mit einem Ton von 1000 Hz und spielen nach einer Weile einen zweiten Ton mit einer Frequenz von 1030 Hz hinzu. Das Bemerkenswerte an diesem Beispiel ist der klar wahrzunehmende Einschwingvorgang der Schwebung bis sie letztendlich bei 30 Schwebungen pro Sekunde angelangt ist. Nichtsdestotrotz nehmen wir dabei aber nur einen einzelnen Ton wahr.
Kehren wir an diesem Punkt wieder zu unserem Klavier zurück und spielen die Töne a' und a'' erst separat und dann zusammen:

a' ⋅⋅ a''
a' + a''

Nun wird das Ohr die Schwebungswahrnehmung nicht mehr haben. Dafür hört es die beiden Töne jedoch klar als zwei voneinander unterschiedliche Gebilde. "Zwischen" ihnen wird nun etwas anderes festgestellt, nicht mehr der Unterschied ihrer sekundlichen Schwingungsmengen, sondern das Verhältnis derselben. Das Ohr stallt fest, dass die beiden Töne zueinender im Verhältnis der sogenannten Oktave stehen. Der Ton a'' hat eine Frequenz von 880 Hz und ist acht diatonische Stufen (am Klavier die weißen Untertasten) vom Ton a' entfernt. Unser Ohr spürt also gleichsam das Zahlenverhältnis 440 ⋅⋅ 880 = 1 ⋅⋅ 2 auf, das ja die Oktave physikalisch kennzeichnet. Das unterscheidende Vergleichen zweier Töne führt zur Schwebungswahrnehmung. Das verhältnisbildende oder messende Vergleichen zweier nun wirklich in der Wahrnehmung getrennten Töne führt zum sogenannten Intervall-Erlebnis. Hier liegt schon keine eigentliche Sinneswahrnehmung mehr vor, sondern ein seelisches Erlebnis auf Grundlage der Sinneswahrnehmung zweier Töne.
Nun lassen wir zu den beiden genannten Tönen noch mindestens einen dritten hinzutreten, etwa denjenigen mit 1760 Schwingungen in der Sekunde (a'''). Wenn drei Töne nacheinander erklingen, liegt die Urform der Skala, der Tonleiter vor. Die Zahlen 440, 880 und 1760 verhalten sich zueinander wie die Zahlen 1, 2 und 4. Das Ohr nimmt naturgemäß nunmehr zwei Oktaven hintereinander wahr; denn die Oktavenwahrnehmung gründete sich auf das Verhältnis 1 ⋅⋅ 2, und dieses waltet in der Zahlenfolge 1, 2 und 4 von 1 nach2 ebenso wie von 2 nach 4. Wir setzen also bei dem Erklingen von mindestens drei Tönen das an Hand zweier Töne gewonnene Intervall-Erlebnis in die Mehrheit der Töne fort. Das Skalen-Erlebnis ist eine Vielfalt von Intervall-Erlebnissen. Aber es ist nicht bloß dieses, sondern mehr. Das einzelne Intervall ist ja ein Vergleich. Die Skala gestattet über den einzelnen Vergleich hinaus das Vergleichen der Intervalle, das Vergleichen der Vergleiche und setzt sich damit in Parallele zu dem mathematischen Gebilde der Proportionen. So beruht das als Beispiel angeführte Skalen-Erlebnis auf der Proportion:

1 ⋅⋅ 2

=

2 ⋅⋅ 4

Das Bemerkenswerte ist bei diesem Vergleichen der Vergleiche, dass die einzelnen Vergleichs-Elemente, die Intervalle nämlich, den Charakter von Schritten, von Tonschritten annehmen. Mehrere Intervalle werden miteinander verglichen, wie man verschiedene Schritte miteinander vergleicht. So sind zwei Oktaven hintereinander für das Ohr der gleiche Tonschritt. Das Vergleichen von Schritten geschieht jedoch im Sinne des Unterschiedsbildens. Aber es würde ja einen Widerspruch ergeben, wenn wir nun daraufhin zwischen den Zahlen 1, 2 und 4 die Unterschiede bilden würden; denn dann würde herauskommen, dass von 1 nach 2 ein anderer Schritt sei als von 2 nach 4, was ja gerade nicht der Fall ist. Das Problem liegt vor, zwischen den drei Zahlen 1, 2 und 4 solche Beziehungen herzustellen, dass die Gleichheit des Tonschrittes von 1 nach 2 mit demjenigen von 2 nach 4 in die Augen springt. Die Lösung liegt darin, die Zahlen 1, 2 und 4 sämtlich in Potenzen einer und derselben Basis, als welche sich hier die Zahl 2 empfiehlt, umzuschreiben. Dann wird aus der Folge 1, 2 und 4 die Folge 2⁰, 2¹ und 2². Die Gleichheit der beiden Tonschritte leuchtet nunmehr in der Folge der Exponenten 0, 1 und 2 auf: von 0 nach 1 ist es derselbe Schritt wie von 1 nach 2. Das Hör-Erlebnis der Skala findet also seinen ihm angemessenen Ausdruck in der Aufeinanderfolge der Exponenten unter Zugrundelegung einer und derselben Basis.
Es ist ganz gleich, welche Basis man dabei wählt. Hätten wir die Basis 4 für unsere Zahlenfolge 1, 2 und 4 gewählt, so hätten die Potenzen gelautet:

40

4½

41

Die neue Exponentenfolge 0, ½ und 1 zeigt wiederum die Gleichheit der beiden Tonschritte. Was tut also unser Ohr im Wahrnehmen der Intervallfolge mehrerer Töne? Es vollzieht einen geheimnisvollen geistigen Akt, welcher dem Verstande als eine Umschmelzung der Schwingungszahlen der einzelnen Töne in Potenzen derselben Basis erscheint. Das musikalische Erlebnis der Skala spielt sich dann sozusagen oben in den Exponenten, d.h. in den Logarithmen der Schwingungszahlen ab. Dabei hält das Ohr die Basis des entstandenen Logarithmensystems im Hintergrunde und befasst sich nur mit dem Abstandsrhythmus, der in der Folge der Logarithmen derselben Basis waltet. Die Proportionalität der verschiedenen Logarithmensysteme zueinander, die wir in Abschnitt 10 kennen lernten und in Abschnitt 11 am logarithmischen Rechenstab verwirklicht fanden, verwirklicht sich noch einmal in dem Vergleichen der Tonschritte der verschiedenen Töne einer Skale.
Welches ist z.B. der zahlenmäßige Ausdruck der Erlebnisses einer Durtonleiter? Da müssen wir zwischen der rein gestimmten und der temperiert gestimmten Skala unterscheiden. Die rein gestimmte Skala liegt vor, wenn sich die Schwingungszahlen der aufeinanderfolgenden acht Töne - z.B. von c' nach c'' - zueinander verhalten wie die Zahlen

24

:

27

:

30

:

32

:

36

:

40

:

45

:

48

Prim

:

Sekunde

:

Terz

:

Quart

:

Quint

:

Sext

:

Septim

:

Oktave

Die reine Stimmung würde sich wie folgt anhören:

Rein gestimmte Tonleiter

Wir schreiben jetzt einfach alles in Potenzen einer und derselben Basis um, am besten so, dass der Prim dem Exponenten 0 (Null) zugeordnet wird. Dies erreichen wir, indem wir alle Zahlen durch 24 teilen, damit an der Stelle der Prim die 1 erscheint, deren Exponent ja bei jeder Basis die Zahl 0 ist:

1

:

9/8

:

5/4

:

4/3

:

3/2

:

5/3

:

15/8

:

2

1

:

1,125

:

1,25

:

1,3

:

1,5

:

1,6

:

1,875

:

2

Von diesen Zahlen berechnen wir am zweckmäßigsten die dyadischen Logarithmen, damit die Oktavzahl 2 den Exponenten 1 erhält:

20

:

20,170

:

20,322

:

20,415

:

20,585

:

20,737

:

20,907

:

21

Die dyadischen Logarithmen gewinnt man ja, indem man die dekadischen Logarithmen mit dem Modul 3,3219 multipliziert (siehe Abschnitt 10!).

Zwischen Prim und Oktave lagern sich demnach Sekunde, Terz, Quart, Quint, Sext und Septim so, wie sich zwischen die Zahlen 0 und 1 die oben errechneten dyadischen Logarithmen lagern. In der Musik hat sich nun eine besondere logarithmische Einheit für die Intervalle durchgesetzt: das Cent [¢]. Der Name kommt daher, dass ein gleichstufiger Halbton in 100 Schritte geteilt wird. Da eine Oktave zwölf Halbtöne umfasst, entspricht sie 1200 Cent. Wenn wir unsere Logarithmen nun also vertausendzweihundertfachen, so heißt die Folge:

0

:

204

:

386

:

498

:

702

:

884

:

1088

:

1200

Die Abstandsfolge dieser Zahlen lautet:

204

182

112

204

182

204

112

In den Musikwissenschaften kennt man diese einzelnen Abstandzahlen als die Intervalle des großen Ganztonschrittes, des kleinen Ganztonschrittes und des Halbtonschrittes:

204			=			großer Ganztonschritt
182			=			kleiner Ganztonschritt
112			=			Halbtonschritt

Für die rein gestimmte C-Dur-Tonleiter lässt sich also zusammenfassend darstellen:

c' ⋅⋅ c'

c' ⋅⋅ d'

c' ⋅⋅ e'

c' ⋅⋅ f'

c' ⋅⋅ g'

c' ⋅⋅ a'

c' ⋅⋅ h'

c' ⋅⋅ c''

Prim

Sekunde

Terz

Quart

Quint

Sext

Septim

Oktave

1

9/8

5/4

4/3

3/2

5/3

15/8

2

0

204

386

498

702

884

1088

1200

204

182

112

204

182

204

112

9/8

10/9

16/15

9/8

10/9

9/8

16/15

c'

d'

e'

f'

g'

a'

h'

c''

wobei die vorletzte Zeile das Frequenzverhältnis benachbarter Töne angibt.
Tragen wir nun die entsprechenden Töne und Intervalle auf einer Frequenzgeraden auf, erhalten wir folgendes Bild:

Deutlicher als zuvor ist nun zu erkennen, dass die Töne der rein gestimmten Tonleiter nicht gleichmäßig über das Frequenzspektrum - und somit über das Tonspektrum - verteilt sind. Unsere C-Dur-Tonleiter hört sich zwar wunderschön an, wollen wir sie aber z.B. um die Note e' herum aufbauen um beispielsweise ein Stück in E-Dur zu spielen, ist sie nicht geeignet. Die Frequenzabstände würden nicht mehr passen und wir müssten unser Klavier komplett umstimmen

Wir können aber versuchsweise einen Akkord in Fis-Dur auf einem in reinem C-Dur gestimmten Klavier spielen. Beginnen wir mit dem reinen C-Dur-Akkord:

C-Dur-Akkord in reiner C-Stimmung

Und nun ein Fis-Dur Akkord auf einem in reinem C-Dur gestimmten Klavier:

Fis-Dur-Akkord in reiner C-Stimmung

Nun ist Fis-Dur harmonisch weit entfernt von C-Dur, die Intervalle sind in diesem Falle also extrem verschoben, d.h. verstimmt, aber es macht das Problem der rein gestimmten Tonleiter sehr gut erfahrbar.
Diese Unflexibilität des rein gestimmten Tonleitersystems war schon in der Antike bekannt gewesen, doch erst als im 15. bis 18. Jahrhundert die Kompositionen immer raffinierter wurden und man damit begann, auch innerhalb eines einzigen Musikstückes die Tonart zu wechseln - der Musiker nennt dies "Modulation" - rang man sich zu einem Kompromiss durch. In der Renaissance entwickelte man zunächst die mitteltönige Stimmung, indem man die Frequenzverhältnisse des großen und kleinen Ganztonschrittes zu einem irrationalen "mittleren" Ganztonschritt verschmolz:

√(9/8 ⋅ 10/9)

=

√5/4

Der neue Halbtonschritt lässt sich ebenfalls mittels der Musiktheorie über das sogenannte syntonisches Komma (Frequenzverhältnis 81/80), die Quart und die reine große Terz herleiten, dies würde jedoch den Rahmen unserer Handlung sprengen. Wir befriedigen uns daher mit dem Endergebnis 117 ¢. Die mitteltönige Stimmung sieht im Vergleich zur reinen nun wie folgt aus:

c'

d'

e'

f'

g'

a'

h'

c''

Intervall [¢]

204

182

112

204

182

204

112

rein

Verhältnis

9/8

10/9

16/15

9/8

10/9

9/8

16/15

rein

Verhältnis

5/4

5/4

XX

5/4

5/4

5/4

XX

mitteltönig

Intervall [¢]

193

193

117

193

193

193

117

mitteltönig

c'

d'

e'

f'

g'

a'

h'

c''

Der Unterschied zwischen großem und kleinem Ganztonschritt ist hinfällig geworden, das System ist flexibler. Dieses Tonleitersystem dominierte das gesamte Barock bis hinein in die Mitte des 18. Jahrhunderts die Musikgeschichte. Durch das Aufkommen zwölfsaitiger und somit zwölfstufiger Tasteninstrumente setzte sich dann jedoch die temperiert gestimmte Skala durch. Bei ihr wird der "Zwischenraum" zwischen der Prim und der Oktav in lauter gleicher Tonschritte unterteilt, und zwar in 12 Halbtonschritte, die sich auf 13 Töne verteilen:

Intervall				Prim				Sekunde				Terz				Quart				Quint				Sext				Septim				Oktave
Tonnummer				1				3				5				6				8				10				12				13

Ein Ganztonschritt umfasst jetzt stets zwei solcher neuen Halbtonschritte, was die Flexibilität des Systems noch weiter erhöht. Die Reihe der Schwingungszahlen dieser einzelnen Töne lautet jetzt:

Prim

:

Sekunde

:

Terz

:

Quart

:

Quint

:

Sext

:

Septim

:

Oktave

20

:

22/12

:

24/12

:

25/12

:

27/12

:

29/12

:

211/12

:

21

20

:

20,167

:

20,333

:

20,417

:

20,583

:

20,750

:

20,917

:

21

Wenn wir die Exponenten, die wieder die dyadischen Logarithmen der einzelnen Schwingungszahlen darstellen, vertausendzweihundertfachen, kommen wir zu der Folge:

0

:

200

:

400

:

500

:

700

:

900

:

1100

:

1200

Die Abstandsfolge dieser Zahlen lautet:

200

200

100

200

200

200

100

Es gibt nur noch Ganztonschritte und Halbtonschritte wie beim mitteltönigen System, aber jetzt bildet der Halbtonschritt wirklich die Hälfte des Ganztonschrittes! Eine wichtige Neuerung, welche dieses Tonleitersystem noch flexibler macht als zuvor. Der Haltonschritt entspricht der Abstandszahl 1/12 bzw. 1200 ⋅ 1/12 = 100, der Ganztonschritt entspricht der doppelten Abstandszahl 2/12 bzw. 1200 ⋅ 2/12 = 200. An dieser Stelle muss gesagt werden, dass dieses "gleichstufig" temperierte Tonleitersystem, welches heute fast alle Klaviere und Tasteninstrumente aufweisen, nicht das durch vorwiegend Johann Sebastian Bach berühmt gewordene "wohltemperierte" Tonleitersystem ist. Das "Bach'sche" System hatte noch unterschiedlich große Quinten und gliedert sich in eine Reihe von Zwischenentwicklungen vom mitteltönigen zum gleichmäßig temperierten System ein, u.a. Entwicklungen von Andreas Werckmeister, vom Bach-Schüler Johann Philipp Kirnberger, von Friedrich Wilhelm Marpurg oder von Johann Georg Neidhardt. Letzendlich hört sich die gleichstufig temperiert gestimmte Tonleiter wie folgt an:

Gleichmäßig temperierte Stimmung

Zum Vergleich noch einmal die reine Stimmung:

Reine Stimmung

Der Unterschied zwischen diesen beiden Tonleitersystemen ist allerdings nur mit einem guten Gehör vernehmbar. Deutlicher wird er bei Akkorden, wie der nächste Vergleich zeigt:

C-Dur Akkord rein
C-Dur Akkord temperiert

Und endlich können wir auch unseren Fis-Dur Akkord richtig gestimmt erklingen lassen!

Fis-Dur Akkord in reiner Stimmung
Fis-Dur Akkord in temperierter Stimmung

Durch den Übergang von der reinen Stimmung zur temperierten ist eine Verlagerung der einzelnen Töne eingetreten, an der die Prim und die Oktave nicht teilgenommen haben. Welchen Umfang diese Verlagerung angenommen hat, ersieht man am besten aus einer Gegenüberstellung der beiderseitigen dyadischen Logarithmen, wobei wir die Vertausendzweihundertfachung beibehalten wollen:

Intervall

Prim

:

Sekunde

:

Terz

:

Quart

:

Quint

:

Sext

:

Septim

:

Oktave

rein

0

:

204

:

386

:

498

:

702

:

884

:

1088

:

1200

temperiert

0

:

200

:

400

:

500

:

700

:

900

:

1100

:

1200

Wir sehen, dass die Terz, die Sext und die Septim die stärksten Verlagerungen erfahren haben, wogegen diejenige der Sekunde, der Quart und der Qint nur gering ist.
Das mit den Logarithmen zusammenhängende Skalen-Erlebnis trägt nicht mehr wie das eine Stufe tieferliegende Intervall-Erlebnis ein bloß seelisches Element in sich, sondern wächst darüber hinaus in eine rein geistige Sphäre hinein. Unsere Dreiheit des Vergleichens, bestehend aus Unterschied, Verhältnis und Logarithmus, weist verborgen in sich auch auf die Urdreiheit des Körperlichen, Seelischen und Geistigen hin.
So tragen wir den Stufenbau des Rechnens als musikalisch veranlagte Wesen bis in unser tiefstes Menschsein hinein. Wie anders werden wir nun einem solchen Gebiete wie der Logarithmenrechnung gegenüberstehen, wenn wir wissen, dass wir beim hörenden Auffassen von Tonleitern oder auch von Akkorden, die mehr als zwei Töne umfassen, etwas tun, was der Herstellung einer Logarithmentafel vergleichbar ist! Wie anders schauen wir nun auch die Tastatur etwa eines Klavieres an, auf der ja die verschiedenen Oktavtasten in räumlich gleichen Abständen voneinanderliegen und auf der die Zwischentöne einer einzelnen Oktave so angeordnet sind, wie es den entwickelten Abstandszahlen einer gleichstufig temperierten Skala entspricht! Wo es sich um einen Ganztonschritt handelt, schaltet sich zwischen zwei weißen Tasten eine schwarze als Veranlasserin des dazwischenliegenden Halbtones ein; wo ein Halbtonschritt vorliegt, folgen zwei weiße Tasten direkt aufeinander. Eine solche Tastatur ist im Grunde nichts anderes als ein ins Musikalische verwandelter logarithmischer Rechenstab. Denken wir uns zu den einzelnen Tasten die Schwingungszahlen der zu ihnen gehörigen Saiten hinzu, so haben wir einen wirklichen logarithmischen Rechenstab vor uns. Bei letzterem lesen wir die Zahlen ab, bei der Tastatur hören wir durch Anschlagen der Tasten die entsprechenden Töne ab.

Was im vorigen als der Zusammenhang zwischen Tonleitererlebnis und dem Logarithmus vor uns stand, sei mathematisch noch etwas weiter geführt. Wir legen wieder unser ursprüngliches Beispiel, wonach vor unserem Ohre aufeinanderfolgende Oktaven erklingen, deren Schwingungszahlen die Zahlen 440, 880, 1760, ⋅⋅⋅⋅ sein mögen, zugrunde. Dann haben wir hörend das Erlebnis gleicher Tonschritte; wir durchschreiten gleichsam die Zahlenfolge 0, 1, 2, ⋅⋅⋅⋅ Welches ist der rechnerische Zusammenhang zwischen beiden Zahlengruppen? Diese Frage wird leicht durch eine Untereinanderstellung der beiden Zahlengruppen beantwortet:

Schwingungszahlen			440		880		1760		3520		7040		⋅⋅⋅⋅⋅		allgemein y
Skalenzahlen			0		1		2		3		4		⋅⋅⋅⋅⋅		allgemein x

Wir erkennen folgenden Zusammenhang:

440		=		440 ⋅ 1		=		440 ⋅ 20
880		=		440 ⋅ 2		=		440 ⋅ 21
1760		=		440 ⋅ 4		=		440 ⋅ 22
3520		=		440 ⋅ 8		=		440 ⋅ 23
7040		=		440 ⋅ 16		=		440 ⋅ 24
⋅⋅⋅⋅⋅
⋅⋅⋅⋅⋅
allgemein:				y		=		440 ⋅ 2x

Diese leicht einsehbare Beziehung wollen wir so umformen, dass nicht y, sondern x, die Skalenzahl, fertig ausgerechnet vor uns steht:

2x		=		y 440				woraus ja hervorgeht:
x		=		dyad. log		y 440

Nun mögen wir unter 440 Schwingungen pro Sekunde eine große Schwingung pro Sekunde verstehen. Dann werden 880 Schwingungen pro Sekunde zwei große Schwingungen pro Sekunde sein, usw., und y gewöhnlichen Schwingungen pro Sekunde werden y/440 große Schwingungen pro Sekunde entsprechen. Dieser Bruch möge durch den Buchstaben Y abgekürzt ausgedrückt werden, so dass also jetzt Y die neue Schwingungszahl in Gestalt der Anzahl großer Schwingungen pro Sekunde bedeutet. Dann hängt die Skalenzahl x mit der zu ihr gehörigen Schwingungszahl Y durch die Beziehung zusammen:

x

=

dyad. log Y

Aber auch die Skalenzahl x wollen wir durch eine andere Skalenzahl X ersetzen. Auf diese kommen wir, wenn wir als Letztes noch den Übergang zu den natürlichen Logarithmen vollziehen. Da mögen wir uns ins Gedächtnis zurückrufen, dass für jede Zahl Y gilt:

dyad. log Y   nat. log Y

=

dyad. log 2   nat. log 2

=

1 0,6931

woraus folgt:

dyad. log Y

=

nat. log Y   0,6931

Dann wird aus unserer Gleichung y = dyad. log Y:

x		=		nat. log Y   0,6931				oder
0,6931 ⋅ x		=		nat. log Y

Das linke Produkt aus den Zahlen 0,6931⋅⋅⋅⋅ und x soll unsere neue Skalenzahl X sein. Dann besteht zwischen der Schwingungszahl Y und der Skalenzahl X die Beziehung:

X		=		nat. log Y				oder, was damit gleichbedeutend ist:
Y		=		eX

In Worten ausgedrückt, sagt diese Beziehung:

Wenn man die Schwingungszahl der Töne einer Skala passend misst und für die Schrittzahlen der Skala ebenfalls eine passende Messung wählt, so erweisen sich diese Schrittzahlen als die natürlichen Logarithmen der Schwingungszahlen!

Was hier für die Wahrnehmung der Tonhöhe als gültig nachgewiesen ist, gilt wunderbarerweise auch für alle möglichen anderen Wahrnehmungen, für Lichtwahrnehmungen, Druckwahrnehmungen, Temperaturwahrnehmungen u.a. Diese wichtige Entdeckung wurde von dem Physiologen und Anatomen Ernst Heinrich Weber, dem Bruder des großen Physikers Wilhelm Weber, im Jahre 1834 gemacht. Es blieb dann dem Physiker Gustav Theodor Fechner vorbehalten, den weittragenden Wert dieser Weber'schen Entdeckung zu erkennen und sie in seinem Ende 1859 herausgegebenen Werke "Elemente der Psychophysik" (2. Auflage im Jahre 1889 von Wilhelm Wundt und 3. Auflage im Jahre 1907 herausgegeben) auszubauen und mathematisch zu untermauern. Seitdem ist dieses Gesetz in den Bestand der psychologischen Wissenschaft unter dem Namen des Weber-Fechner'schen Gesetzes eingegangen. Fechner nennt obige Formel die Maßformel und sagt in seiner Terminologie:

»In Worte übersetzt lautet die Maßformel:
Die Größe der Empfindung steht im Verhältnis nicht zu der absoluten Größe des Reizes, sondern zu dem Logarithmus der Größe des Reizes, wenn dieser auf seinen Schwellenwert, d.i. diejenige Größe als Einheit bezogen wird, bei welcher die Empfindung entsteht oder verschwindet, oder kurz, sie ist proportional dem Logarithmus des fundamentalen Reizwertes.«

Was Fechner hier als "die Größe der Empfindung" bezeichnet, war in unserem Beispiel die Schrittzahl x der Skalenwahrnehmung. Als "Größe des Reizes" figurierte bei uns die Schwingungszahl y. Unter dem "Schwellenwert" wäre die Zahl 440 zu verstehen, weil bei dieser Anzahl von Schwingungen das Skalenerlebnis entsteht oder verschwindet. Indem wir den sogenannten Reizwert y auf den sogenannten Schwellenwert 440 beziehen, gelangen wir zu dem "fundamentalen Reizwert" Y = y/440. Es ist hier nicht der Ort, auf den Sinn der andersartigen Bezeichnungen Fechner's einzugehen. Es muss uns genügen, die Übereinstimmung des Weber-Fechner'schen Gesetzes mit dem zwischen Schwingungszahlen und Skalenzahlen waltenden Gesetze eingesehen zu haben.

Durch die Untersuchungen dieses letzten Abschnittes werden alle bisherigen Ausführungen auf einen Gipfelpunkt geführt. Stufe um Stufe enträtselte sich uns das Wesen Logarithmus, bis wir zuletzt erkannten, wie er in der Welt der Empfindungen des Menschen waltet, wenn die Außenwelt, an ihn heranbrandend, ihre Wirkungen in die Tiefe der Sinne hineinschickt. Ein Vermittler zwischen Innenwelt und Außenwelt ist er. Wenn der Mensch das, was er in seinem Geiste ersinnt, der Außenwelt zuführt, um es praktisch werden zu lassen, hat er keinen treueren Gehilfen als den Logarithmus. Aber nicht minder ist er der Bote, wenn dieselbe Außenwelt sich in Gestalt von Empfindungen im Innern des Menschen spiegelt. Von hier aus gesehen, kann uns auch sein Name, der die beiden Begriffe logos und arithmos zueinanderführt, in einem neuen Glanze erscheinen.
Dieser Glanz würde noch zunehmen, wenn auf den Logarithmus das volle Licht der höheren mathematischen Betrachtungsweise fiele. Eine Probe davon bot sich uns bereits dar, als wir uns manche Ergebnisse dieser höheren Betrachtungsweise, soweit sie mit Hilfe elementarer Begriffe, wenn auch nicht begründet, so doch wenigstens beschrieben werden können, vor Augen hielten, wie z.B. die Eigenschaften der Loxodrome oder der unterschiedlichen Spiralen. Aber es gibt noch viele Eigenschaften dieses Logarithmus, zu deren bloßer Beschreibung auch die gewöhnlichen Begriffe nicht mehr ausreichen. Auf ihre Kenntnis und Erkenntnis müssen wir hier verzichten, uns damit begnügen, eingesehen zu haben, dass schon durch das gewöhnliche Denken der menschliche Geist in die Tiefen dieses bedeutsamen Gebildes zu dringen vermag.

Ebenso wie dieser letzte Abschnitt mit Frédéric Chopin begonnen hat, lassen wir ihn auch wieder ausklingen. Passend hierzu ist ein Stück aus seiner Klaviersonate Nr. 2 in b-Moll, Opus 35, die er 1839 komponierte. Es handelt sich dabei um den "Marche funèbre", den Trauermarsch, denn dies ist la

---