Bei der Recherche und Arbeit an »Logarithmen für alle!« bin ich über die Geschichte der Entwicklung unseres Tonleitersystems gestolpert, die ich im 16. und letzten Abschnitt dieser »Logarithmen-Saga« angekratzt hatte. Schon damals erwähnte ich darin, dass die ganze Geschichte eindeutig den Rahmen der dortigen Handlung sprengen würde. Die ganze Geschichte zu erzählen sei Kulturhistorikern und Musikwissenschaftlern vorbehalten, da diese über die dazu notwendige Kompetenz verfügen, hier jedoch soll nun auf einen mathematisch sehr interessanten Teilaspekt eingegangen werden: Die Entwicklung des mitteltönig gestimmten Tonleitersystems aus dem reinen Stimmungssystem. Während das letztgenannte System die Musikgeschichte bis zur Renaissance beherrschte, war das erstgenannte der Wegbereiter zu unserem heute vorwiegend genutzten gleichstufig temperierten Stimmungssytem.
Dimostrationi harmoniche
Der Weg zum Mittelton
Inhalt
Einleitung
Der Quintenzirkel in Dur und Moll
Teil I - Die Anfänge
Pythagoras in der Schmiede
[ back ]
Um den Faden unserer Diskussion aus »Logarithmen für alle!« an der passenden Stelle wieder aufzunehmen und ihn in eine andere Richtung weiterzuspinnen, sei hier wiederholt, dass sich die rein gestimmte C-Dur Tonleiter zahlenmäßig wie folgt darstellen lässt:
c' ⋅⋅ c' |
|
c' ⋅⋅ d' |
|
c' ⋅⋅ e' |
|
c' ⋅⋅ f' |
|
c' ⋅⋅ g' |
|
c' ⋅⋅ a' |
|
c' ⋅⋅ h' |
|
c' ⋅⋅ c'' |
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
1 |
|
9/8 |
|
5/4 |
|
4/3 |
|
3/2 |
|
5/3 |
|
15/8 |
|
2 |
0 |
|
204 |
|
386 |
|
498 |
|
702 |
|
884 |
|
1088 |
|
1200 |
| |
204 |
|
182 |
|
112 |
|
204 |
|
182 |
|
204 |
|
112 |
|
| |
9/8 |
|
10/9 |
|
16/15 |
|
9/8 |
|
10/9 |
|
9/8 |
|
16/15 |
|
c' |
|
d' |
|
e' |
|
f' |
|
g' |
|
a' |
|
h' |
|
c'' |
Dabei stellen die ersten beiden Zahlenfolgen die Tonabstände der einzelnen Töne (c', d', e', f', ⋅⋅⋅⋅) zum Grundton dieser Tonleiter selbst (c') als Verhältnis und in der üblichen logarithmischen Einheit Cent [¢] dar; die letzten beiden Zahlenfolgen bilden sich aus den Schrittweiten dieser Tonabstände in Cent und als Verhältnis ausgedrückt, oder in anderen Worten ausgedrückt, es sind die relativen Tonabstände von den jeweiligen Tönen (c', d', e', f', ⋅⋅⋅⋅) zum nächsten und umgekehrt.
Auf einer Frequenzgerade sieht letzteres ungefähr so aus:
Wieder erkennen wir deutlich, dass die einzelnen Töne c', d', e', f', ⋅⋅⋅⋅ nicht gleichmäßig über die Frequenzgerade verteilt sind. Wir erkennen zwei große Schrittweiten und eine kleinere, die etwa halb so groß ist wie die beiden anderen. Daher nennt man diese Schritte:
204 |
|
|
= |
|
|
großer Ganztonschritt |
182 |
|
|
= |
|
|
kleiner Ganztonschritt |
112 |
|
|
= |
|
|
Halbtonschritt |
Inklusive der Halbtöne, die auf einem Klavier oder anderem Tasteninstrument mit Hilfe der schwarzen Tasten zu finden sind, hört sich die reine Stimmung so an:

| Rein gestimmte Tonleiter |
|
|
|
 |
Bis hierher handelte es sich um eine Wiederholung aus »Logarithmen für alle!«.
Nun wollen wir unsere Frequenzgerade aufwickeln, wie es das Bild zur Rechten zeigt, und die Halbtöne mit in unsere Überlegungen einbeziehen! Die Halbtöne werden in der Musik mit dem  (sprich »b«) und mit dem
(sprich »b«) und mit dem  (sprich »Kreuz«) gekennzeichnet. Das
(sprich »Kreuz«) gekennzeichnet. Das  erniedrigt den Ton um einen Halbtonschritt und verleiht der Notenbezeichnung die Nachsilbe »es« - aus »d« wird »des« - und das
erniedrigt den Ton um einen Halbtonschritt und verleiht der Notenbezeichnung die Nachsilbe »es« - aus »d« wird »des« - und das  erhöht den jeweiligen Ton um einen Halbtonschritt und verleiht der Notenbezeichnung die Nachsilbe »is« - aus »d« wird »dis«.
erhöht den jeweiligen Ton um einen Halbtonschritt und verleiht der Notenbezeichnung die Nachsilbe »is« - aus »d« wird »dis«.
An dieser Stelle wollen wir ein kleines Geheimnis lüften. Als ich als kleiner Bub mit der Musik anfing, fragte ich mich, warum die Bezeichnungen der Stammtöne C, D, E, F, G, A und H so unlogisch vom Alphabet A, B, C, D, E, F und G abweichen. Auf das »A« sollte gefälligst das »B« folgen, und nicht das »H«! Bis zum Mittelalter war das auch tatsächlich so; auf »A« folgte ganz natürlich das »B«, die sieben Töne wären völlig ausreichend. Doch spätestens mit dem Benediktinermönch Guido von Arezzo (* um 992; † unsicher: 17. Mai 1050) änderte sich dies. Er etablierte die Spaltung des Tones B in eine höhere Variante, die er »b durum« nannte, und in eine tiefere Variante, die er - wir erahnen es - »b molle« nannte. Dabei gab er dem erstgenannten Ton das Zeichen »b quadratum« 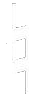 und dem letztgenannten das Zeichen »b rotundum«
und dem letztgenannten das Zeichen »b rotundum«  mit auf den Weg. Nur glich dieses
mit auf den Weg. Nur glich dieses 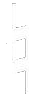 unserem heutigen »h«, welches aus den beiden etrusker'schen Schreibweisen
unserem heutigen »h«, welches aus den beiden etrusker'schen Schreibweisen  und
und  hervorging, die sich einreihten in die proto-semitische,
hervorging, die sich einreihten in die proto-semitische,  , und phönizer'sche Schreibweise,
, und phönizer'sche Schreibweise, , und mit der Zeit verwandelte sich das
, und mit der Zeit verwandelte sich das 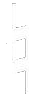 in ein »h«. Als dann noch im 15. Jahrhundert der Buchdruck erfunden wurde, wurde auch dieser Trend durch die Verwendung der Drucktype h abgeschlossen. Im angelsächsischen Sprachraum heißt unser »H« übrigens noch heute »B«, während dort unser »B« (also die Erniedrigung des H um einen Halbton) »B flat« genannt wird.
in ein »h«. Als dann noch im 15. Jahrhundert der Buchdruck erfunden wurde, wurde auch dieser Trend durch die Verwendung der Drucktype h abgeschlossen. Im angelsächsischen Sprachraum heißt unser »H« übrigens noch heute »B«, während dort unser »B« (also die Erniedrigung des H um einen Halbton) »B flat« genannt wird.
Wie dem auch sei, durch diese Exkursion haben wir auch erfahren, wie die Begriffe »Dur« und »Moll« entstanden sind, zwei Begriffe, die noch wichtig werden.
Aber zurück zu unserer Frequenzgeraden, die in ihrem aufgewickelten Zustand lieber Frequenzkreis oder Frequenzzirkel genannt werden sollte: Wir wollen nun alle Töne der eingestrichenen Tonleiter auf diesem Kreis wiederfinden, die unser Klavier zu bieten hat, also auch die Halbtöne der schwarzen Tasten. Reizvoll harmonisch und auch für einen völligen Anfänger nicht zu schwer zu spielen, ist folgende Reihenfolge:
Wir starten also bei c' und gehen eine Quint - vier weiße Tasten - nach rechts bis zum g', von dort eine Quart - drei weiße Tasten - nach links bis zum d', wieder eine Quint nach rechts zum a' usw. Wenn wir beim h' angekommen sind, gehen wir eine Quart nach links und landen auf der schwarzen Taste fis', was gleichbedeutend mit dem ges' ist. Von dort gehen wir wieder eine Quart nach links bis zum des', was wiederum gleichbedeutend mit dem cis' ist. Von dort gehen wir eine Quint nach rechts bis zum as', nun eine Quart nach links bis zum es' usw. über das b', f' bis zum c, wo wir enden. Beim c haben wir die Wahl zwischen dem c'' und dem c'. Um den Kreis zu schließen, wählen wir das c'.
 Nun tragen wir die diese Tonreihenfolge auf unserem Frequenzzirkel auf, den wir von nun an lieber Quinten- oder Quartenzirkel nennen wollen, da die Reihenfolge der Töne durch Quinten und Quarten entstanden ist. Das Ergebnis sehen wir links.
Nun tragen wir die diese Tonreihenfolge auf unserem Frequenzzirkel auf, den wir von nun an lieber Quinten- oder Quartenzirkel nennen wollen, da die Reihenfolge der Töne durch Quinten und Quarten entstanden ist. Das Ergebnis sehen wir links.
Das man den Quintenzirkel auch eleganter vertonen kann, zeigt Frédéric Chopin in seinem Nocturne, Opus 37, Nr. 2. Darin findet sich kurz vor Schluss, Takt 129 bis 132, eine dreitaktige Passage, in welcher die Harmoniegrundtöne im Bass alle zwölf Stationen des Quintenzirkels (abwärts) durchlaufen:
| Frédéric Chopin: Nocturne, Opus 37, Nr. 2, Takt 129 bis 132 |
|
|
|
 |
Und nun wird es leicht kompliziert. Dieser Schritt ist aber notwendig um zu begreifen, vor welchen Problemen die Musiker damals standen. Wir wollen nun versuchen, zu all diesen Tönen in unserem Quintenzirkel eine eigene Tonleiter zu finden und dabei den Rhythmus »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton« beizubehalten!
Da wir die Tonleiter vom Grundton c ja als Ausgangspunkt unserer Überlegung schon haben, versuchen wir es zunächst mit dem ihm folgenden Grundton g:
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| |
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
GT |
|
HT |
|
g |
|
a |
|
h |
|
c |
|
d |
|
e |
|
f |
|
g |
Der Rhytmus passt bis zur Septim. Dort finden wir von e nach f einen Halbtonschritt anstatt eines geforderten Ganztonschrittes vor, während der darauf folgende Schritt von f nach g ein ganzer satt eines halben ist. Wenn wir f nun mit einem  etwas nach rechts verrücken, würde der Rhythmus wieder stimmen. Wir haben nun also:
etwas nach rechts verrücken, würde der Rhythmus wieder stimmen. Wir haben nun also:
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
g |
|
a |
|
h |
|
c |
|
d |
|
e |
|
 f |
|
g |
Damit zufrieden gehen wir zum nächsten Ton über, dem d, und finden nun:
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| |
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
GT |
|
HT |
|
d |
|
e |
|
 f |
|
g |
|
a |
|
h |
|
c |
|
d |
Wieder ist es die Septim, die sich dem Rhythmus aus dem gleichen Grunde widersetzt wie zuvor, also verfahren wir auch auf gleicher Weise und erhalten:
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
d |
|
e |
|
 f |
|
g |
|
a |
|
h |
|
 c |
|
d |
Wir sehen also ein Muster vor uns: Beim Übergang zum im Quintenzirkel folgenden Grundton der jeweiligen Tonleiter widersetzt sich die Septim dem »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton«-Rhythmus. Dieses »Septim-Problem« lösen wir, indem wir den dazu gehörigen Ton mit einem  nach rechts versetzen. Behalten wir diese Vorgehensweise über die zwölf Stufen des Quintenzirkels bei, erhalten wir:
nach rechts versetzen. Behalten wir diese Vorgehensweise über die zwölf Stufen des Quintenzirkels bei, erhalten wir:
| |
|
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| 1. |
|
c |
|
d |
|
e |
|
f |
|
g |
|
a |
|
h |
|
c |
| 2. |
|
g |
|
a |
|
h |
|
c |
|
d |
|
e |
|
 f |
|
g |
| 3. |
|
d |
|
e |
|
 f |
|
g |
|
a |
|
h |
|
 c |
|
d |
| 4. |
|
a |
|
h |
|
 c |
|
d |
|
e |
|
 f |
|
 g |
|
a |
| 5. |
|
e |
|
 f |
|
 g |
|
a |
|
h |
|
 c |
|
 d |
|
e |
| 6. |
|
h |
|
 c |
|
 d |
|
e |
|
 f |
|
 g |
|
 a |
|
h |
| 7. |
|
 f |
|
 g |
|
 a |
|
h |
|
 c |
|
 d |
|
 e |
|
 f |
| 8. |
|
 c |
|
 d |
|
 e |
|
 f |
|
 g |
|
 a |
|
 h |
|
 c |
| 9. |
|
 g |
|
 a |
|
 h |
|
 c |
|
 d |
|
 e |
|
  f |
|
 g |
| 10. |
|
 d |
|
 e |
|
  f |
|
 g |
|
 a |
|
 h |
|
  c |
|
 d |
| 11. |
|
 a |
|
 h |
|
  c |
|
 d |
|
 e |
|
  f |
|
  g |
|
 a |
| 12. |
|
 e |
|
  f |
|
  g |
|
 a |
|
 h |
|
  c |
|
  d |
|
 e |
| 13. |
|
 h |
|
  c |
|
  d |
|
 e |
|
  f |
|
  g |
|
  a |
|
 h |
| |
|
|
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
GT |
|
HT |
|
Rein formal ist dies zwar durchaus richtig und hat seine Berechtigung, aber 
 sieht doch schon etwas seltsam aus. Nun ist eine Erhöhung um zwei Halbtöne im Grunde aber gleichbedeutend mit der Erhöhung um einen Ganzton! Unsere Tabelle würde demnach so aussehen:
sieht doch schon etwas seltsam aus. Nun ist eine Erhöhung um zwei Halbtöne im Grunde aber gleichbedeutend mit der Erhöhung um einen Ganzton! Unsere Tabelle würde demnach so aussehen:
| |
|
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| 1. |
|
c |
|
d |
|
e |
|
f |
|
g |
|
a |
|
h |
|
c |
| 2. |
|
g |
|
a |
|
h |
|
c |
|
d |
|
e |
|
 f |
|
g |
| 3. |
|
d |
|
e |
|
 f |
|
g |
|
a |
|
h |
|
 c |
|
d |
| 4. |
|
a |
|
h |
|
 c |
|
d |
|
e |
|
 f |
|
 g |
|
a |
| 5. |
|
e |
|
 f |
|
 g |
|
a |
|
h |
|
 c |
|
 d |
|
e |
| 6. |
|
h |
|
 c |
|
 d |
|
e |
|
 f |
|
 g |
|
 a |
|
h |
| 7. |
|
 f |
|
 g |
|
 a |
|
h |
|
 c |
|
 d |
|
 e |
|
 f |
| 8. |
|
 c |
|
 d |
|
 e |
|
 f |
|
 g |
|
 a |
|
 h |
|
 c |
| 9. |
|
 g |
|
 a |
|
 h |
|
 c |
|
 d |
|
 e |
|
g |
|
 g |
| 10. |
|
 d |
|
 e |
|
g |
|
 g |
|
 a |
|
 h |
|
d |
|
 d |
| 11. |
|
 a |
|
 h |
|
d |
|
 d |
|
 e |
|
g |
|
a |
|
 a |
| 12. |
|
 e |
|
g |
|
a |
|
 a |
|
 h |
|
d |
|
e |
|
 e |
| 13. |
|
 h |
|
d |
|
e |
|
 e |
|
g |
|
a |
|
h |
|
 h |
| |
|
|
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
GT |
|
HT |
|
Als nächstes beachten wir, dass die Schritte h ⋅⋅ c und e ⋅⋅ f sowieso schon Halbtonschritte sind, dass also  h und
h und  e nichts weiter als c und f sind.
e nichts weiter als c und f sind.
| |
|
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| 1. |
|
c |
|
d |
|
e |
|
f |
|
g |
|
a |
|
h |
|
c |
| 2. |
|
g |
|
a |
|
h |
|
c |
|
d |
|
e |
|
 f |
|
g |
| 3. |
|
d |
|
e |
|
 f |
|
g |
|
a |
|
h |
|
 c |
|
d |
| 4. |
|
a |
|
h |
|
 c |
|
d |
|
e |
|
 f |
|
 g |
|
a |
| 5. |
|
e |
|
 f |
|
 g |
|
a |
|
h |
|
 c |
|
 d |
|
e |
| 6. |
|
h |
|
 c |
|
 d |
|
e |
|
 f |
|
 g |
|
 a |
|
h |
| 7. |
|
 f |
|
 g |
|
 a |
|
h |
|
 c |
|
 d |
|
 e |
|
 f |
| 8. |
|
 c |
|
 d |
|
f |
|
 f |
|
 g |
|
 a |
|
c |
|
 c |
| 9. |
|
 g |
|
 a |
|
c |
|
 c |
|
 d |
|
f |
|
g |
|
 g |
| 10. |
|
 d |
|
f |
|
g |
|
 g |
|
 a |
|
c |
|
d |
|
 d |
| 11. |
|
 a |
|
c |
|
d |
|
 d |
|
f |
|
g |
|
a |
|
 a |
| 12. |
|
f |
|
g |
|
a |
|
 a |
|
c |
|
d |
|
e |
|
f |
| 13. |
|
c |
|
d |
|
e |
|
f |
|
g |
|
a |
|
h |
|
c |
| |
|
|
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
GT |
|
HT |
|
Zu guter letzt erinnern wir uns an die Identitäten  c =
c =  d,
d,  d =
d =  e,
e,  f =
f =  g,
g,  g =
g =  a und
a und  a =
a =  h oder eben b und erhalten letztendlich die Tabelle:
h oder eben b und erhalten letztendlich die Tabelle:
| |
|
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| 1. |
|
c |
|
d |
|
e |
|
f |
|
g |
|
a |
|
h |
|
c |
| 2. |
|
g |
|
a |
|
h |
|
c |
|
d |
|
e |
|
 f |
|
g |
| 3. |
|
d |
|
e |
|
 f |
|
g |
|
a |
|
h |
|
 c |
|
d |
| 4. |
|
a |
|
h |
|
 c |
|
d |
|
e |
|
 f |
|
 g |
|
a |
| 5. |
|
e |
|
 f |
|
 g |
|
a |
|
h |
|
 c |
|
 d |
|
e |
| 6. |
|
h |
|
 c |
|
 d |
|
e |
|
 f |
|
 g |
|
 a |
|
h |
| 7. |
|
 f |
|
 g |
|
 a |
|
h |
|
 c |
|
 d |
|
 e |
|
 f |
| 8. |
|
(  g) |
|
(  a) |
|
(  h) |
|
(  c) |
|
(  d) |
|
(  e) |
|
(f) |
|
(  g) |
| 9. |
|
 d |
|
 e |
|
f |
|
 g |
|
 a |
|
 h |
|
c |
|
 d |
| 10. |
|
 a |
|
 h |
|
c |
|
 d |
|
 e |
|
f |
|
g |
|
 a |
| 11. |
|
 e |
|
f |
|
g |
|
 a |
|
 h |
|
c |
|
d |
|
 e |
| 12. |
|
 h |
|
c |
|
d |
|
 e |
|
f |
|
g |
|
a |
|
 h |
| 13. |
|
f |
|
g |
|
a |
|
 h |
|
c |
|
d |
|
e |
|
f |
| 14. |
|
c |
|
d |
|
e |
|
f |
|
g |
|
a |
|
h |
|
c |
| |
|
|
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
GT |
|
HT |
|
In dieser letzten Tabelle ist die 8. Zeile hinzugekommen. Diese Zeile entsteht durch eine komplette enharmonische Verwechlung mit der 7. Zeile, d.h. dank der Erhöhung oder Erniedrigung durch das  oder
oder  hören sich zwar die Töne der 7. und 8. Zeile gleich an, die Noten an sich sind aber durchgehend verschieden zueinander.
hören sich zwar die Töne der 7. und 8. Zeile gleich an, die Noten an sich sind aber durchgehend verschieden zueinander.
Und nun erinnern wir uns, dass wir zu Beginn dieser Arbeit damit begonnen hatten, die Septim einer jeden Tonleiter mit einem  zu versehen um den gewünschten »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton«-Rhythmus beibehalten zu können. Dieses
zu versehen um den gewünschten »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton«-Rhythmus beibehalten zu können. Dieses  , oder eigentlich ja
, oder eigentlich ja 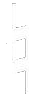 , kennzeichnete ursprünglich die höhere Variante der Note »B«, das »b durum«. Aus diesem Grunde nennt man diese Tonleiterzusammenstellung das »Dur-System«. Der zu Grunde liegende »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton«-Rhythmus ist demnach auch der »Dur-Rhythmus«.
Nun hat sich in den Musikwissenschaften eingebürgert, die Dur-Tonleitern mit Großbuchstaben zu kennzeichnen. Wir schreiben unsere Tabelle also nach dieser Konvention neu auf und benennen die einzelnen Tonleitern nach ihrer jeweiligen Anfangs- und Endnote:
, kennzeichnete ursprünglich die höhere Variante der Note »B«, das »b durum«. Aus diesem Grunde nennt man diese Tonleiterzusammenstellung das »Dur-System«. Der zu Grunde liegende »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton«-Rhythmus ist demnach auch der »Dur-Rhythmus«.
Nun hat sich in den Musikwissenschaften eingebürgert, die Dur-Tonleitern mit Großbuchstaben zu kennzeichnen. Wir schreiben unsere Tabelle also nach dieser Konvention neu auf und benennen die einzelnen Tonleitern nach ihrer jeweiligen Anfangs- und Endnote:
| |
|
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| C-Dur |
|
C |
|
D |
|
E |
|
F |
|
G |
|
A |
|
H |
|
C |
| G-Dur |
|
G |
|
A |
|
H |
|
C |
|
D |
|
E |
|
 F |
|
G |
| D-Dur |
|
D |
|
E |
|
 F |
|
G |
|
A |
|
H |
|
 C |
|
D |
| A-Dur |
|
A |
|
H |
|
 C |
|
D |
|
E |
|
 F |
|
 G |
|
A |
| E-Dur |
|
E |
|
 F |
|
 G |
|
A |
|
H |
|
 C |
|
 D |
|
E |
| H-Dur |
|
H |
|
 C |
|
 D |
|
E |
|
 F |
|
 G |
|
 A |
|
H |
| Fis-Dur |
|
 F |
|
 G |
|
 A |
|
H |
|
 C |
|
 D |
|
 E |
|
 F |
| (Ges-Dur) |
|
(  G) |
|
(  A) |
|
(B) |
|
(  C) |
|
(  D) |
|
(  E) |
|
(F) |
|
(  G) |
| Des-Dur |
|
 D |
|
 E |
|
F |
|
 G |
|
 A |
|
B |
|
C |
|
 D |
| As-Dur |
|
 A |
|
B |
|
C |
|
 D |
|
 E |
|
F |
|
G |
|
 A |
| Es-Dur |
|
 E |
|
F |
|
G |
|
 A |
|
B |
|
C |
|
D |
|
 E |
| B-Dur |
|
B |
|
C |
|
D |
|
 E |
|
F |
|
G |
|
A |
|
B |
| F-Dur |
|
F |
|
G |
|
A |
|
B |
|
C |
|
D |
|
E |
|
F |
| C-Dur |
|
C |
|
D |
|
E |
|
F |
|
G |
|
A |
|
H |
|
C |
| |
|
|
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
GT |
|
HT |
|
Nun stellt sich natürlich die Frage, wie das Moll-System zustande kommt. Im Prinzip nach denselben Spielregeln wie das Dur-System. Das Moll-System hat lediglich einen anderen Grundrhythmus, nämlich »Ganzton - Halbton - Ganzton - Ganzton - Halbton - Ganzton - Ganzton«. Augenscheinlich ist auf dem Klavier der Grundton »a« die einzige Möglichkeit diesen Rhythmus zu erhalten, ohne die schwarzen Tasten zu Hilfe zu nehmen:
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| |
GT |
|
HT |
|
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
a |
|
h |
|
c |
|
d |
|
e |
|
f |
|
g |
|
a |
Wie beim Dur-System zuvor gehen wir nun eine Quint zur nächsten Note, aber dieses Mal nach links zum »d«:
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| |
GT |
|
HT |
|
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
d |
|
e |
|
f |
|
g |
|
a |
|
h |
|
c |
|
d |
Das »Septim-Problem« des »Dur-Systems« hat sich zur Sext verlagert. Dort finden wir einen Ganztonschritt von der Quint zur Sext anstatt des erwünschten Halbtonschrittes und einen Halbtonschritt von der Sext zur Septim anstelle des erwünschten Ganztonschrittes vor. Dieses neue »Sext-Problem« lösen wir, indem wir die Sext mit einem  erniedrigen.
erniedrigen.
Und wie wir nun schon vermutet haben, entdecken wir das »Sext-Problem« auch bei der nächsten Tonleiter, die wir erhalten, wenn wir vom »d« eine weitere Quint nach links zum »g« gehen:
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| |
GT |
|
HT |
|
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
g |
|
a |
|
 h |
|
c |
|
d |
|
e |
|
f |
|
g |
Wir sehen also was als nächstes zu tun ist, und gehen frisch zur Tat. Am Ende sollte unser »Moll-Tonleitersystem« wie folgt aussehen:
| |
|
Prim |
|
Sekunde |
|
Terz |
|
Quart |
|
Quint |
|
Sext |
|
Septim |
|
Oktave |
| a-Moll |
|
a |
|
h |
|
c |
|
d |
|
e |
|
f |
|
g |
|
a |
| d-Moll |
|
d |
|
e |
|
f |
|
g |
|
a |
|
b |
|
c |
|
d |
| g-Moll |
|
g |
|
a |
|
b |
|
c |
|
d |
|
 e |
|
f |
|
g |
| c-Moll |
|
c |
|
d |
|
 e |
|
f |
|
g |
|
 a |
|
b |
|
c |
| f-Moll |
|
f |
|
g |
|
 a |
|
b |
|
c |
|
 d |
|
 e |
|
f |
| b-Moll |
|
b |
|
c |
|
 d |
|
 e |
|
f |
|
 g |
|
 a |
|
b |
| es-Moll |
|
 e |
|
f |
|
 g |
|
 a |
|
b |
|
 c |
|
 d |
|
 e |
| (dis-Moll) |
|
(  d) |
|
(  e) |
|
(  f) |
|
(  g) |
|
(  a) |
|
(h) |
|
(  c) |
|
(  d) |
| gis-Moll |
|
 g |
|
 a |
|
h |
|
 c |
|
 d |
|
e |
|
 f |
|
 g |
| cis-Moll |
|
 c |
|
 d |
|
e |
|
 f |
|
 g |
|
a |
|
h |
|
 c |
| fis-Moll |
|
 f |
|
 g |
|
a |
|
h |
|
 c |
|
d |
|
e |
|
 f |
| h-Moll |
|
h |
|
 c |
|
d |
|
e |
|
 f |
|
g |
|
a |
|
h |
| e-Moll |
|
e |
|
 f |
|
g |
|
a |
|
h |
|
c |
|
d |
|
e |
| a-Moll |
|
a |
|
h |
|
c |
|
d |
|
e |
|
f |
|
g |
|
a |
| |
|
|
GT |
|
HT |
|
GT |
|
GT |
|
HT |
|
GT |
|
GT |
|
Wenn wir dies nun zu unserem ursprünglichen Quintenzirkel dazutragen, erkennen wir eine wunderbare Konsistenz wenn wir das Moll-System mit »a-Moll« auf 12 Uhr startend, entgegen des Uhrzeigersinns laufen lassen.
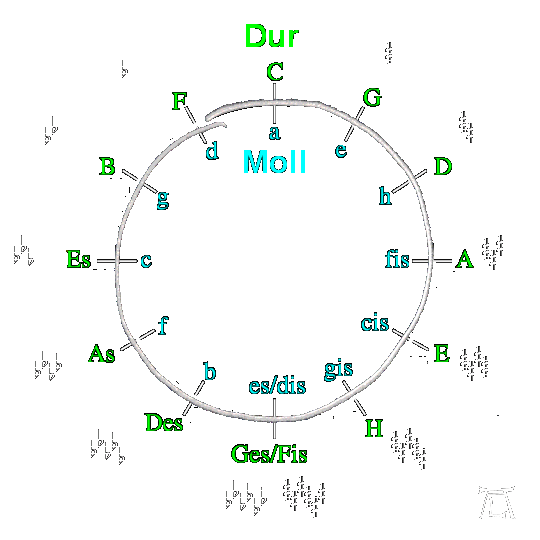 Nicht nur die Anzahl der
Nicht nur die Anzahl der  s und
s und  e stimmen, wie zu erwarten war, überein, sondern auch die Lage bzw. Position derselben im Notensystem selbst. Dies ist übrigens eine Eigenschaft des Quintenzirkels, die mich als kleiner Bub stets an die Natürlichkeit dieses Ordnungssystems zweifeln ließ. Und in der Tat ist der Quintenzirkel nur auf Grund einer entscheidenen Rahmenbedingung möglich:
e stimmen, wie zu erwarten war, überein, sondern auch die Lage bzw. Position derselben im Notensystem selbst. Dies ist übrigens eine Eigenschaft des Quintenzirkels, die mich als kleiner Bub stets an die Natürlichkeit dieses Ordnungssystems zweifeln ließ. Und in der Tat ist der Quintenzirkel nur auf Grund einer entscheidenen Rahmenbedingung möglich:
Der Quintenzirkel ist nur auf Grund von temperierten Stimmungen und ihrer Möglichkeit zur enharmonischen Umdeutung von Tönen denkbar!
Beispielsweise würde in einer Stimmung mit theoretisch reinen Quinten, wie die pythagoreischen Stimmung, der Vorläufer der reinen Stimmung, die wiederum auch reine Terzen aufweist, kein geschlossener Quintenzirkel verwirklicht werden können. So umschließen zwölf Quinten (c-g-d-a-e-h- f-
f- c-
c- g-
g- d-
d- a-
a- e-
e- h) ein Intervall von circa sieben Oktaven. Nimmt man die Quinten und Oktaven mit ihren reinen Schwingungszahlverhältnissen 3:2 und 2:1 an, so lässt sich berechnen, dass der Abschlusston
h) ein Intervall von circa sieben Oktaven. Nimmt man die Quinten und Oktaven mit ihren reinen Schwingungszahlverhältnissen 3:2 und 2:1 an, so lässt sich berechnen, dass der Abschlusston  h der Quintenreihe geringfügig (um ca. einen Achtelton) höher ist als das gleichzeitig erreichte letzte c der Oktavenreihe. Dieser Unterschied, pythagoreisches Komma genannt, verhindert die Gleichsetzung von
h der Quintenreihe geringfügig (um ca. einen Achtelton) höher ist als das gleichzeitig erreichte letzte c der Oktavenreihe. Dieser Unterschied, pythagoreisches Komma genannt, verhindert die Gleichsetzung von  h und c sowie aller anderen, ebenfalls um das pythagoreische Komma verschiedenen, enharmonischen Tonpaare (
h und c sowie aller anderen, ebenfalls um das pythagoreische Komma verschiedenen, enharmonischen Tonpaare ( f/
f/ g,
g,  d/
d/ e,
e,  a/
a/ h usw.). Die Quintenfolge schließt sich somit nicht zum Kreis, sondern lässt sich nur als Spirale darstellen. Würde man dessen ungeachtet versuchen, den Kreis »mit Gewalt« zu schließen, so ginge das nur über eine sogenannte Wolfsquinte.
h usw.). Die Quintenfolge schließt sich somit nicht zum Kreis, sondern lässt sich nur als Spirale darstellen. Würde man dessen ungeachtet versuchen, den Kreis »mit Gewalt« zu schließen, so ginge das nur über eine sogenannte Wolfsquinte.
Das Problem, die Quintenspirale ohne solche misstönenden Wolfsquinten zum Kreis zu schließen, wird bei der heute verbreiteten gleichstufig temperierten Stimmung dadurch gelöst, dass man jede der zwölf Quinten um 1/12 des pythagoreischen Kommas verkleinert, so dass man mit dem zwölften Quintschritt exakt zur siebten Okave des Ausgangstons gelangt. Durch die gleichmäßige Verteilung des Kommas wird erreicht, dass zwar außer der Oktave kein Intervall mehr ganz rein klingt, die Unsauberkeiten jedoch so gering bleiben, dass sie kaum noch stören.
Genau dies soll der Inhalt dieser Geschichte sein, die »Dimostrationi harmoniche - Der Weg zum Mittelton«.
Eine antike Legende, die an den Waldorfschulen gerne erzählt wird, besagt, dass Pythagoras eines Tages an einer Schmiede vorbeikam, in der vier Handwerker mit Hämmern bei der Arbeit waren. Dieses Bild muss wohl auch damals schon beruhigend gewesen sein, denn Pythagoras hielt inne und lauschte andächtig den Hammerklängen. Dabei bemerkte er, dass die einzelnen Schläge Töne unterschiedlicher Tonhöhe hervorriefen, die paarweise Harmonien ergaben. Dabei konnte er Oktave, Quinte und Quarte unterscheiden. Nur ein Paar, welches das Intervall zwischen Quarte und Quinte (große Sekunde) ergab, empfand er als dissonant.
Daraufhin lief er freudig an den verdutzten Handwerker vorbei und in die Schmiede hinein, um selbst Versuche mit unterschiedlichen Hämmern anzustellen. Während seiner Hämmerei fand er heraus, dass der Unterschied in der Tonhöhe weder von der Gestalt des Hammers noch von der Lage des geschlagenen Eisens oder der Kraft des Schlags abhängt. Vielmehr konnte er die Tonhöhen den Gewichten der Hämmer zuordnen, die er dann genau maß und zueinander ins Verhältnis setzte:

| Schwerer Hammer |
|
|
|
 |
|
|
|
Schwerer Hammer Leichter Hammer |
|
= |
|
2 |
| Mittelschwerer Hammer |
|
|
|
 |
|
|
|
Mittelschwerer Hammer Leichter Hammer |
|
= |
|
3/2 |
| Mittelleichter Hammer |
|
|
|
 |
|
|
|
Mittelleichter Hammer Leichter Hammer |
|
= |
|
4/3 |
| Leichter Hammer |
|
|
|
 |
|
|
|
Leichter Hammer Leichter Hammer |
|
= |
|
1 |
Der Legende zur Folge, kehrte er dann zutiefst beglückt heim. Nach dem Abendessen hängte er an einem Pflock, der schräg über die Ecke an den Wänden befestigt war, der Reihe nach vier gleich lange, gleich starke und gleich gedrehte Saiten auf, die er unten durch Anbinden unterschiedlicher Gewichte beschwerte. Dann schlug er die Saiten paarweise an, wobei die gleichen Harmonien erklangen wie in der Schmiede. Die mit zwölf Gewichtseinheiten am stärksten beschwerte Saite ergab mit der am geringsten belasteten, an der sechs Gewichtseinheiten hingen, eine Oktave. So zeigte sich, dass die Oktave auf dem Verhältnis 12 : 6, also 2 : 1 beruht. Die gespannteste Saite ergab mit der zweitlockersten (acht Gewichtseinheiten) eine Quinte, mit der zweitstraffsten (neun Gewichtseinheiten) eine Quarte. Daraus folgte, dass die Quinte auf dem Verhältnis 12 : 8, also 3 : 2 beruht, die Quarte auf dem Verhältnis 12 : 9, also 4 : 3. Für das Verhältnis der zweitstraffsten Saite zur lockersten ergab sich wiederum mit 9 : 6, also 3 : 2, eine Quinte, für das der zweitlockersten zur lockersten mit 8 : 6, also 4 : 3, eine Quarte. Für das dissonante Intervall zwischen Quinte und Quarte zeigte sich, dass es auf dem Verhältnis 9 : 8 beruht, was mit den schon in der Schmiede durchgeführten Gewichtsmessungen übereinstimmte. Die Oktave erwies sich als das Produkt von Quinte und Quarte:
Nun dehnte Pythagoras den Versuch auf verschiedene Instrumente aus, experimentierte mit Gefäßen, Flöten, Triangeln, dem Monochord usw.; dabei fand er immer die gleichen Zahlenverhältnisse. Schließlich führte er die seither geläufigen Benennungen für die relativen Tonhöhen ein. Das Gebiet der Musikwissenschaften ward geboren!
Ob diese Legende nun auf wahre Begebenheiten beruht, sei einmal dahingestellt, sie enthält aber viel Wahres. So waren den »pre-Pythagoras'schen« Idäischen Daktylen zufolge die mythischen Erfinder der Schmiedekunst auch die Erfinder der Musik, da sie als Kenner des Geheimnisses der magischen Musik dargestellt wurden. Die Legende von Pythagoras in der Schmiede ist somit eine späte Umformung und Rationalisierung des uralten Daktylen-Mythos: In der Pythagoras-Legende erscheinen die Schmiede nicht mehr als Besitzer alten magischen Wissens, sondern sie werden ohne es zu wollen zu (unwissenden) »Lehrmeistern« des Pythagoras. Im Frühmittelalter bezeichnete Isidor von Sevilla den biblischen Schmied Tubal als den Erfinder der Musik; darin folgten ihm spätere Autoren. In dieser Überlieferung zeigt sich wiederum die Vorstellung einer Beziehung zwischen Schmiedekunst und Musik, die auch in außereuropäischen Mythen und Sagen vorkommt.
Auch das Pythagoras, den wir vor allem durch seine mathematischen Arbeiten und dem »Satzes des Pythagoras« wegen kennen, der erste Mensch war, der die Töne der Musik nachweislich in eine systematische Ordnung gebracht hat, ist eine Tatsache. Nach ihm ist die »pythagoras'sche Stimmung« benannt, mit der wir uns zu Beginn beschäftigen wollen. Dazu benutzte er zwar keine Hämmer, aber das Monochord.




![]() (sprich »b«) und mit dem
(sprich »b«) und mit dem ![]() (sprich »Kreuz«) gekennzeichnet. Das
(sprich »Kreuz«) gekennzeichnet. Das ![]() erniedrigt den Ton um einen Halbtonschritt und verleiht der Notenbezeichnung die Nachsilbe »es« - aus »d« wird »des« - und das
erniedrigt den Ton um einen Halbtonschritt und verleiht der Notenbezeichnung die Nachsilbe »es« - aus »d« wird »des« - und das ![]() erhöht den jeweiligen Ton um einen Halbtonschritt und verleiht der Notenbezeichnung die Nachsilbe »is« - aus »d« wird »dis«.
erhöht den jeweiligen Ton um einen Halbtonschritt und verleiht der Notenbezeichnung die Nachsilbe »is« - aus »d« wird »dis«.![]() und dem letztgenannten das Zeichen »b rotundum«
und dem letztgenannten das Zeichen »b rotundum« ![]() mit auf den Weg. Nur glich dieses
mit auf den Weg. Nur glich dieses ![]() unserem heutigen »h«, welches aus den beiden etrusker'schen Schreibweisen
unserem heutigen »h«, welches aus den beiden etrusker'schen Schreibweisen ![]() und
und ![]() hervorging, die sich einreihten in die proto-semitische,
hervorging, die sich einreihten in die proto-semitische, ![]() , und phönizer'sche Schreibweise,
, und phönizer'sche Schreibweise,![]() , und mit der Zeit verwandelte sich das
, und mit der Zeit verwandelte sich das ![]() in ein »h«. Als dann noch im 15. Jahrhundert der Buchdruck erfunden wurde, wurde auch dieser Trend durch die Verwendung der Drucktype h abgeschlossen. Im angelsächsischen Sprachraum heißt unser »H« übrigens noch heute »B«, während dort unser »B« (also die Erniedrigung des H um einen Halbton) »B flat« genannt wird.
in ein »h«. Als dann noch im 15. Jahrhundert der Buchdruck erfunden wurde, wurde auch dieser Trend durch die Verwendung der Drucktype h abgeschlossen. Im angelsächsischen Sprachraum heißt unser »H« übrigens noch heute »B«, während dort unser »B« (also die Erniedrigung des H um einen Halbton) »B flat« genannt wird.
 Nun tragen wir die diese Tonreihenfolge auf unserem Frequenzzirkel auf, den wir von nun an lieber Quinten- oder Quartenzirkel nennen wollen, da die Reihenfolge der Töne durch Quinten und Quarten entstanden ist. Das Ergebnis sehen wir links.
Nun tragen wir die diese Tonreihenfolge auf unserem Frequenzzirkel auf, den wir von nun an lieber Quinten- oder Quartenzirkel nennen wollen, da die Reihenfolge der Töne durch Quinten und Quarten entstanden ist. Das Ergebnis sehen wir links.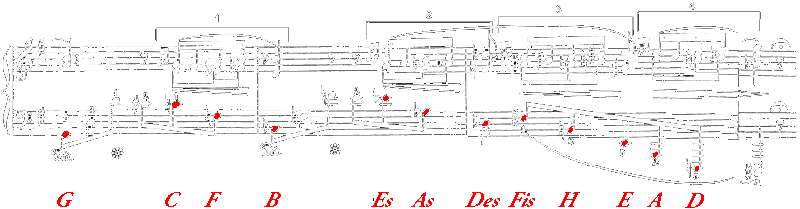
![]() etwas nach rechts verrücken, würde der Rhythmus wieder stimmen. Wir haben nun also:
etwas nach rechts verrücken, würde der Rhythmus wieder stimmen. Wir haben nun also:![]() f
f![]() f
f![]() f
f![]() c
c![]() nach rechts versetzen. Behalten wir diese Vorgehensweise über die zwölf Stufen des Quintenzirkels bei, erhalten wir:
nach rechts versetzen. Behalten wir diese Vorgehensweise über die zwölf Stufen des Quintenzirkels bei, erhalten wir:![]() f
f![]() f
f![]() c
c![]() c
c![]() f
f![]() g
g![]() f
f![]() g
g![]() c
c![]() d
d![]() c
c![]() d
d![]() f
f![]() g
g![]() a
a![]() f
f![]() g
g![]() a
a![]() c
c![]() d
d![]() e
e![]() f
f![]() c
c![]() d
d![]() e
e![]() f
f![]() g
g![]() a
a![]() h
h![]() c
c![]() g
g![]() a
a![]() h
h![]() c
c![]() d
d![]() e
e![]()
![]() f
f![]() g
g![]() d
d![]() e
e![]()
![]() f
f![]() g
g![]() a
a![]() h
h![]()
![]() c
c![]() d
d![]() a
a![]() h
h![]()
![]() c
c![]() d
d![]() e
e![]()
![]() f
f![]()
![]() g
g![]() a
a![]() e
e![]()
![]() f
f![]()
![]() g
g![]() a
a![]() h
h![]()
![]() c
c![]()
![]() d
d![]() e
e![]() h
h![]()
![]() c
c![]()
![]() d
d![]() e
e![]()
![]() f
f![]()
![]() g
g![]()
![]() a
a![]() h
h![]()
![]() sieht doch schon etwas seltsam aus. Nun ist eine Erhöhung um zwei Halbtöne im Grunde aber gleichbedeutend mit der Erhöhung um einen Ganzton! Unsere Tabelle würde demnach so aussehen:
sieht doch schon etwas seltsam aus. Nun ist eine Erhöhung um zwei Halbtöne im Grunde aber gleichbedeutend mit der Erhöhung um einen Ganzton! Unsere Tabelle würde demnach so aussehen:![]() f
f![]() f
f![]() c
c![]() c
c![]() f
f![]() g
g![]() f
f![]() g
g![]() c
c![]() d
d![]() c
c![]() d
d![]() f
f![]() g
g![]() a
a![]() f
f![]() g
g![]() a
a![]() c
c![]() d
d![]() e
e![]() f
f![]() c
c![]() d
d![]() e
e![]() f
f![]() g
g![]() a
a![]() h
h![]() c
c![]() g
g![]() a
a![]() h
h![]() c
c![]() d
d![]() e
e![]() g
g![]() d
d![]() e
e![]() g
g![]() a
a![]() h
h![]() d
d![]() a
a![]() h
h![]() d
d![]() e
e![]() a
a![]() e
e![]() a
a![]() h
h![]() e
e![]() h
h![]() e
e![]() h
h![]() h und
h und ![]() e nichts weiter als c und f sind.
e nichts weiter als c und f sind.![]() f
f![]() f
f![]() c
c![]() c
c![]() f
f![]() g
g![]() f
f![]() g
g![]() c
c![]() d
d![]() c
c![]() d
d![]() f
f![]() g
g![]() a
a![]() f
f![]() g
g![]() a
a![]() c
c![]() d
d![]() e
e![]() f
f![]() c
c![]() d
d![]() f
f![]() g
g![]() a
a![]() c
c![]() g
g![]() a
a![]() c
c![]() d
d![]() g
g![]() d
d![]() g
g![]() a
a![]() d
d![]() a
a![]() d
d![]() a
a![]() a
a![]() c =
c = ![]() d,
d, ![]() d =
d = ![]() e,
e, ![]() f =
f = ![]() g,
g, ![]() g =
g = ![]() a und
a und ![]() a =
a = ![]() h oder eben b und erhalten letztendlich die Tabelle:
h oder eben b und erhalten letztendlich die Tabelle:![]() f
f![]() f
f![]() c
c![]() c
c![]() f
f![]() g
g![]() f
f![]() g
g![]() c
c![]() d
d![]() c
c![]() d
d![]() f
f![]() g
g![]() a
a![]() f
f![]() g
g![]() a
a![]() c
c![]() d
d![]() e
e![]() f
f![]() g)
g)![]() a)
a)![]() h)
h)![]() c)
c)![]() d)
d)![]() e)
e)![]() g)
g)![]() d
d![]() e
e![]() g
g![]() a
a![]() h
h![]() d
d![]() a
a![]() h
h![]() d
d![]() e
e![]() a
a![]() e
e![]() a
a![]() h
h![]() e
e![]() h
h![]() e
e![]() h
h![]() h
h![]() oder
oder ![]() hören sich zwar die Töne der 7. und 8. Zeile gleich an, die Noten an sich sind aber durchgehend verschieden zueinander.
hören sich zwar die Töne der 7. und 8. Zeile gleich an, die Noten an sich sind aber durchgehend verschieden zueinander.![]() zu versehen um den gewünschten »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton«-Rhythmus beibehalten zu können. Dieses
zu versehen um den gewünschten »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton«-Rhythmus beibehalten zu können. Dieses ![]() , oder eigentlich ja
, oder eigentlich ja ![]() , kennzeichnete ursprünglich die höhere Variante der Note »B«, das »b durum«. Aus diesem Grunde nennt man diese Tonleiterzusammenstellung das »Dur-System«. Der zu Grunde liegende »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton«-Rhythmus ist demnach auch der »Dur-Rhythmus«.
Nun hat sich in den Musikwissenschaften eingebürgert, die Dur-Tonleitern mit Großbuchstaben zu kennzeichnen. Wir schreiben unsere Tabelle also nach dieser Konvention neu auf und benennen die einzelnen Tonleitern nach ihrer jeweiligen Anfangs- und Endnote:
, kennzeichnete ursprünglich die höhere Variante der Note »B«, das »b durum«. Aus diesem Grunde nennt man diese Tonleiterzusammenstellung das »Dur-System«. Der zu Grunde liegende »Ganzton - Ganzton - Halbton - Ganzton - Ganzton - Ganzton - Halbton«-Rhythmus ist demnach auch der »Dur-Rhythmus«.
Nun hat sich in den Musikwissenschaften eingebürgert, die Dur-Tonleitern mit Großbuchstaben zu kennzeichnen. Wir schreiben unsere Tabelle also nach dieser Konvention neu auf und benennen die einzelnen Tonleitern nach ihrer jeweiligen Anfangs- und Endnote:![]() F
F![]() F
F![]() C
C![]() C
C![]() F
F![]() G
G![]() F
F![]() G
G![]() C
C![]() D
D![]() C
C![]() D
D![]() F
F![]() G
G![]() A
A![]() F
F![]() G
G![]() A
A![]() C
C![]() D
D![]() E
E![]() F
F![]() G)
G)![]() A)
A)![]() C)
C)![]() D)
D)![]() E)
E)![]() G)
G)![]() D
D![]() E
E![]() G
G![]() A
A![]() D
D![]() A
A![]() D
D![]() E
E![]() A
A![]() E
E![]() A
A![]() E
E![]() E
E![]() erniedrigen.
erniedrigen.![]() h
h![]() e
e![]() e
e![]() a
a![]() a
a![]() d
d![]() e
e![]() d
d![]() e
e![]() g
g![]() a
a![]() e
e![]() g
g![]() a
a![]() c
c![]() d
d![]() e
e![]() d)
d)![]() e)
e)![]() f)
f)![]() g)
g)![]() a)
a)![]() c)
c)![]() d)
d)![]() g
g![]() a
a![]() c
c![]() d
d![]() f
f![]() g
g![]() c
c![]() d
d![]() f
f![]() g
g![]() c
c![]() f
f![]() g
g![]() c
c![]() f
f![]() c
c![]() f
f![]() f
f Nicht nur die Anzahl der
Nicht nur die Anzahl der ![]() s und
s und ![]() e stimmen, wie zu erwarten war, überein, sondern auch die Lage bzw. Position derselben im Notensystem selbst. Dies ist übrigens eine Eigenschaft des Quintenzirkels, die mich als kleiner Bub stets an die Natürlichkeit dieses Ordnungssystems zweifeln ließ. Und in der Tat ist der Quintenzirkel nur auf Grund einer entscheidenen Rahmenbedingung möglich:
e stimmen, wie zu erwarten war, überein, sondern auch die Lage bzw. Position derselben im Notensystem selbst. Dies ist übrigens eine Eigenschaft des Quintenzirkels, die mich als kleiner Bub stets an die Natürlichkeit dieses Ordnungssystems zweifeln ließ. Und in der Tat ist der Quintenzirkel nur auf Grund einer entscheidenen Rahmenbedingung möglich:![]() f-
f-![]() c-
c-![]() g-
g-![]() d-
d-![]() a-
a-![]() e-
e-![]() h) ein Intervall von circa sieben Oktaven. Nimmt man die Quinten und Oktaven mit ihren reinen Schwingungszahlverhältnissen 3:2 und 2:1 an, so lässt sich berechnen, dass der Abschlusston
h) ein Intervall von circa sieben Oktaven. Nimmt man die Quinten und Oktaven mit ihren reinen Schwingungszahlverhältnissen 3:2 und 2:1 an, so lässt sich berechnen, dass der Abschlusston ![]() h der Quintenreihe geringfügig (um ca. einen Achtelton) höher ist als das gleichzeitig erreichte letzte c der Oktavenreihe. Dieser Unterschied, pythagoreisches Komma genannt, verhindert die Gleichsetzung von
h der Quintenreihe geringfügig (um ca. einen Achtelton) höher ist als das gleichzeitig erreichte letzte c der Oktavenreihe. Dieser Unterschied, pythagoreisches Komma genannt, verhindert die Gleichsetzung von ![]() h und c sowie aller anderen, ebenfalls um das pythagoreische Komma verschiedenen, enharmonischen Tonpaare (
h und c sowie aller anderen, ebenfalls um das pythagoreische Komma verschiedenen, enharmonischen Tonpaare (![]() f/
f/![]() g,
g, ![]() d/
d/![]() e,
e, ![]() a/
a/![]() h usw.). Die Quintenfolge schließt sich somit nicht zum Kreis, sondern lässt sich nur als Spirale darstellen. Würde man dessen ungeachtet versuchen, den Kreis »mit Gewalt« zu schließen, so ginge das nur über eine sogenannte Wolfsquinte.
h usw.). Die Quintenfolge schließt sich somit nicht zum Kreis, sondern lässt sich nur als Spirale darstellen. Würde man dessen ungeachtet versuchen, den Kreis »mit Gewalt« zu schließen, so ginge das nur über eine sogenannte Wolfsquinte.